

問題では,まず試行の内容をよくつかみ,
これからマルコフ過程の漸化式自体を自分で作り,
それを解くことで確率を求めるという型ものであることが多い.
このような場合に大切なことは,
![]() 回の試行の後に起こりうるすべての状態に対してその確率を数列におく,
ということである.
そのうえで,
回の試行の後に起こりうるすべての状態に対してその確率を数列におく,
ということである.
そのうえで,![]() 回の試行の後の状態が,
回の試行の後の状態が,
![]() 回の試行の後の状態からどのように定まるのかをつかみ,
それを漸化式にする.
回の試行の後の状態からどのように定まるのかをつかみ,
それを漸化式にする.
状態に対して確率を文字でおく場合,
必要な状態を記述できればよいのでいろいろと工夫し,
できるだけ簡単にしてよい.
いずれにせよ例え具体的な番号に関する確率であっても,
必ず一般の![]() に対する漸化式を立てる.
これを銘記しよう.
に対する漸化式を立てる.
これを銘記しよう.
![]() があり頂点ABCは時計回りに並んでいる.
点
があり頂点ABCは時計回りに並んでいる.
点 ![]() ははじめ点 A にある.
サイコロを投げ1か2が出れば時計回りに隣の頂点に移り,
3〜6が出れば反時計回りに隣の頂点に移る.
ははじめ点 A にある.
サイコロを投げ1か2が出れば時計回りに隣の頂点に移り,
3〜6が出れば反時計回りに隣の頂点に移る.
![]() 回の試行の後に
回の試行の後に ![]() が点Aにいる確率を求めよ.
が点Aにいる確率を求めよ.
考え方
このような問題では
![]() 回の試行の後に
回の試行の後に ![]() が点A,B,Cにいる確率をそれぞれ
が点A,B,Cにいる確率をそれぞれ
![]() とする.
とする.
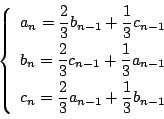
これを基本的な不変関係として,解く.
解き方はいろいろあるが,ここでは![]() だけの漸化式を作って解いてみよう.
3項間漸化式になると予想して
だけの漸化式を作って解いてみよう.
3項間漸化式になると予想して![]() のところからはじめる.
のところからはじめる.
解答
![]() を消去する.
を消去する.
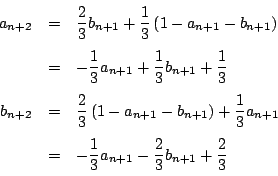
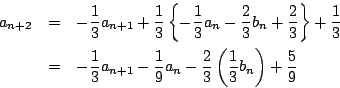
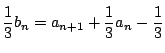 を代入して整理すると
を代入して整理すると
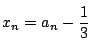 とおく.
とおく.
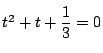 を解いて
を解いて
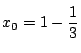 ,
,
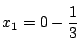 を代入して整理する.
を代入して整理する.
なお
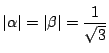 なので
なので
![]() である.これから,
である.これから,