となる. ■
まず次の補題を示す.
証明
![]() とおく.
このとき,
とおく.
このとき,
証明
点![]() を中心とする半径
を中心とする半径![]() の円周
の円周![]() は
は![]() の内部にあるとする.
の内部にあるとする.
![]() 上の点Pと
上の点Pと![]() 上の点Qを結び,
矢線の様に,点Pから点Qへ,点Qから
上の点Qを結び,
矢線の様に,点Pから点Qへ,点Qから![]() 上を反時計回りに点Qに至り,
点Qから点Pへ,そして点Pから
上を反時計回りに点Qに至り,
点Qから点Pへ,そして点Pから![]() 上を時計回りに点Pに至る経路で
次の定積分を行う.ただし,
上を時計回りに点Pに至る経路で
次の定積分を行う.ただし,![]() は
は![]() 上を時計回りにまわる経路である.
積分定理によって,
上を時計回りにまわる経路である.
積分定理によって,
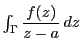 は
は
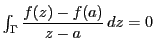 となり,
となり,
証明
点![]() を中心とする円で,その内部で正則であるような半径の最大値を
を中心とする円で,その内部で正則であるような半径の最大値を![]() とする.
とする.
![]() である
である![]() と
と![]() に対して,
に対して,
![]() である点
である点![]() と,
と,![]() を中心とする半径
を中心とする半径![]() の円
の円![]() をとる.
をとる.
![]() が
が![]() 上にあるとき,
上にあるとき,
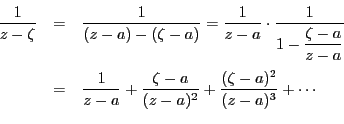
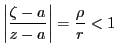 であるから,この等比数列は収束する.
さらに,
であるから,この等比数列は収束する.
さらに,
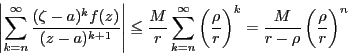
![[*]](images/crossref.gif) によって一様収束する.
この結果
によって一様収束する.
この結果
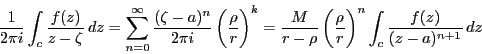
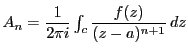 とおくと,
とおくと,
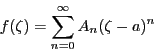
このように,![]() は
は![]() の近傍で冪級数に展開されるので,
の近傍で冪級数に展開されるので,![]() において何回でも微分可能である.
□
において何回でも微分可能である.
□
このように,複素関数を考えるとき,その微分や積分は大きく統制された姿を現す. 冪級数で表される関数を解析関数というとすれば, 実関数の範囲では微分可能性と解析関数であることは同値ではないが, 複素関数の世界ではこれが同値になるのである.
ここから複素関数の世界は大きく展開する. それは他書にゆだねて,本稿はここまでとする.