さらに,曲線![]() が,有限個の点を除いて滑らかであるとき,
つまり有限個の点を除いて
が,有限個の点を除いて滑らかであるとき,
つまり有限個の点を除いて![]() が微分可能であるとき,
このときこれを区分的に滑らかという.
これは対応する
が微分可能であるとき,
このときこれを区分的に滑らかという.
これは対応する![]() 上の曲線が区分的に滑らかであることと同値である.
上の曲線が区分的に滑らかであることと同値である.
分割![]() を上記のようにとり,
点
を上記のようにとり,
点![]() と点
と点![]() で切られる曲線
で切られる曲線![]() の部分上にある
の部分上にある![]() に対応する点
に対応する点![]() を選んで,
和
を選んで,
和
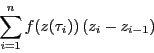
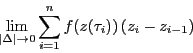
証明
![]() ,
,
![]() ,
,
![]() とする.
このとき
とする.
このとき
![\begin{eqnarray*}
&&f(z(\tau_i))\left(z_i-z_{i-1}\right)\\
&=&P(\xi_i,\ \eta_...
..._i,\ \eta_i)(y_i-y_{i-1})-Q(\xi_i,\ \eta_i)(x_i-x_{i-1})\right]
\end{eqnarray*}](images/img196.gif)
![[*]](images/crossref.gif) によって,
によって,
この極限値を![]() の
の![]() に沿う積分といい
に沿う積分といい
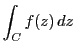 と表す.
と表す.
![]() の
の![]() に沿う積分
に沿う積分
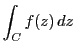 を,
を,
![]() ,
,![]() を明示して
を明示して
![]() が
が![]() で微分可能とする.
複素平面の曲線
で微分可能とする.
複素平面の曲線![]() を実2次元平面の曲線と見なすと,
上記関係式からただちに
を実2次元平面の曲線と見なすと,
上記関係式からただちに
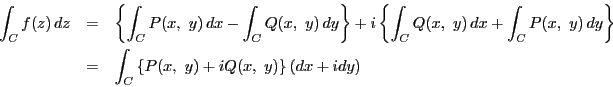
また,積分路![]() の逆向きの曲線を
の逆向きの曲線を![]() とすると
とすると
複素関数の曲線に沿う定積分は,実2次元上の関数の曲線に沿う2つの線積分の組であり, またこれはリーマン和による定積分の思想的範疇に属するものである.
その証明を2通りに行う.
証明1
根拠となるのは,注(![[*]](images/crossref.gif) )に述べたグリーンの定理
)に述べたグリーンの定理![[*]](images/crossref.gif) のグルサによる一般化である.
のグルサによる一般化である.
![]() で囲まれた領域を
で囲まれた領域を![]() とする.
とする.
![]() とする.
とする.![]() が正則なので
が正則なので
![\begin{eqnarray*}
\int_C\left(Pdx-Qdy \right)&=&
\int \!\!\! \int_{[C]}\left(-...
...l P}{\partial x}-\dfrac{\partial Q}{\partial y} \right)\,dxdy=0
\end{eqnarray*}](images/img215.gif)
![[*]](images/crossref.gif) )にあるグルサによる一般化を用いている.
このために,本稿としては自己完結していない.
この方向では,本稿で証明したグリーンの定理(定理
)にあるグルサによる一般化を用いている.
このために,本稿としては自己完結していない.
この方向では,本稿で証明したグリーンの定理(定理![[*]](images/crossref.gif) )の範囲内では証明できない.
ここでもし,定理5の
)の範囲内では証明できない.
ここでもし,定理5の![[*]](images/crossref.gif) )から帰結される.
)から帰結される.
しかし![]() の連続性は逆にコーシーの積分定理からの帰結として導かれる.
したがって
の連続性は逆にコーシーの積分定理からの帰結として導かれる.
したがって![]() の連続性を条件としないでコーシーの積分定理を証明したい.
の連続性を条件としないでコーシーの積分定理を証明したい.
それが次の方法であり,これは『解析概論』[#!______1!#]や『函数論』[#!_________!#]の方法である.
まずいくつかの補題を示す.
証明 曲線
![]() は連続であるから定理
は連続であるから定理![[*]](images/crossref.gif) により,
により,
![]() で一様連続である.つまり
で一様連続である.つまり
![]() で
で
![]() なら
なら
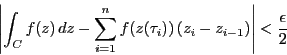
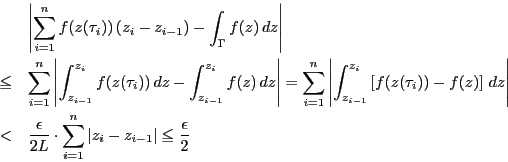
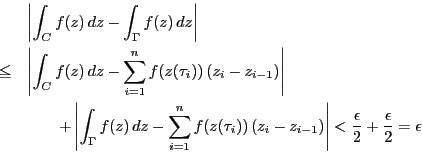
始点と終点の一致する折れ線を閉折れ線という. 同様に閉多角形折れ線も用いる.
2つの折れ線があり,第一の折れ線の始点と,第二の折れ線の始点をつなぐと新たな折れ線ができる. これを折れ線の和という.逆に一つの折れ線を,辺と辺の交点までの折れ線と, そこからはじまる折れ線の和に分けることができる.
一つの折れ線の間にある2つの頂点を線分で結ぶ.これによってその折れ線は その線分を互いに逆の方向に通過する2つの折れ線に分けることができる.
この2つをいずれも折れ線の分解という.
折れ線![]() が
折れ線
が
折れ線
![]() に分解されているとき,
に分解されているとき,
証明 曲線
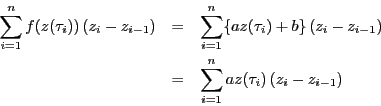
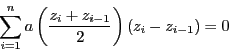
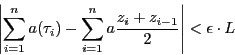
以上の準備のうえに,定理5の第2の証明を行う.
証明2
曲線![]() の上の1点
の上の1点![]() とる.
とる.![]() から
から![]() に至る任意の折れ線
に至る任意の折れ線
![]() に関して
に関して
補題2によって,閉三角形折れ線![]() に関して,
に関して,
閉三角形折れ線![]() を辺の中点を結ぶ線を新たな辺として4つに分解する.
これを繰りかえして
を辺の中点を結ぶ線を新たな辺として4つに分解する.
これを繰りかえして![]() を
を![]() 個に分解する.
個に分解する.
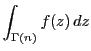 であるとする.
つまり
であるとする.
つまり
であるようにすることができる.![]() の決め方から,
の決め方から,
![]() のとき
のとき
![]() は
は![]() の周か内部にあり,したがってその極限
の周か内部にあり,したがってその極限![]() も
も
![]() の周か内部にある.
また
の周か内部にある.
また![]() の周か内部の2点間の距離は,その周の長さに
の周か内部の2点間の距離は,その周の長さに
![]() を超えることはない.
つまり,
を超えることはない.
つまり,![]() の周か内部の任意の点
の周か内部の任意の点![]() に
対して
に
対して
補題3より第一項の積分値は0である.また
![\begin{displaymath}
\left\vert\int_{\Gamma(n)}\left[\eta(z)\cdot(z-c)\right]\,d...
...}\cdot\dfrac{L}{2^n}\cdot\dfrac{L}{2^n}=\dfrac{\epsilon}{4^N}
\end{displaymath}](images/img264.gif)
この証明はここでは行わない.