- 1.
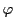 は
は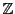 上の全単射写像である.
上の全単射写像である.
- 2.
-
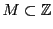 かつ
かつ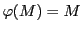 ならば
ならば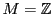 である.
である.
- 3.
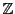 は無限集合である.
は無限集合である.
青空学園の『数論初歩』の「存在と構成」では自然数の公理から整数を構成した.自然数をすべての基礎とする考え方は,西洋の伝統である.これに対して,高木貞治の最後の著作となった『数の概念』では,整数の定義からはじまる.意識されていたのかどうかはわからないが,二つの方向の数を対等に扱う東洋的な数の世界をふまえた公理系が示されている.そして,それはより根底的で明晰である.
西洋数学では,あくまで自然数が基礎であり,負数や有理数は必要のために導かれるという立場である.つまり正の数こそ存在する第一のものであり,負数はそこから導かれるという立場である.これにたいして,『数の概念』における定義は,最初から負数も含めた整数の定義である.
また,高木貞治は「我々の整数は,物の数でもなく,物の順序を示すものでもない」(『数の概念』)という立場で整数を定義する.その立場では,数とはいわゆる基数としての数,また順序数としての数のいずれでもない.高木貞治が上記公理系で定義した数が,集合論と結びついて基数ともなり,また順序を定めるものともなる.これは世界的にも他にない一般的な考え方である.
この歴史的,文化的な問題に関しては『数とは何か そしてまた何であったか』[23]に詳しい.『数の概念』の公理系と,それにもとづく整数の定義をここに紹介する.
整数の公理を考えることは,我々の整数のすべての性質を導くのに,最小限どのような公理が必要であるかを考えることである.
『数論初歩』のペアノの公理で![]() の操作にあたるのが
の操作にあたるのが![]() である.高木の定義とペアノノ公理が結びつく.これから整数の諸性質を導くことは,基本的には『数論初歩』でやったのと同じことであるが,その骨子は次のようになされる.証明はつけないので,定理としては掲げない.
である.高木の定義とペアノノ公理が結びつく.これから整数の諸性質を導くことは,基本的には『数論初歩』でやったのと同じことであるが,その骨子は次のようになされる.証明はつけないので,定理としては掲げない.
![]() の要素
の要素![]() に対して
に対して
の二つの要素
に関して次のいずれか一つが成立する.
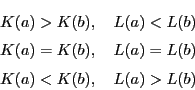
それぞれに応じて![]() の大小を
の大小を
![]() で
で![]() または
または![]() が成り立つ記号とすれば,
が成り立つ記号とすれば,![]() は順序の定義4に従う.つまり整数の大小関係
は順序の定義4に従う.つまり整数の大小関係![]() は順序であり,集合
は順序であり,集合![]() は全順序集合である.
しかし,この関係
は全順序集合である.
しかし,この関係![]() で
で![]() は整列集合ではない.
は整列集合ではない.
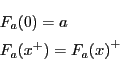
この証明は![]() に関する数学的帰納法でなされる.
に関する数学的帰納法でなされる.
![]() のとき.
のとき.![]() とすると条件を満たし,かつこれ以外にないことが
とすると条件を満たし,かつこれ以外にないことが![]() に関する数学的帰納法で示される.その上で,
に関する数学的帰納法で示される.その上で,![]() の存在を仮定して
の存在を仮定して![]() と
と![]() を
を
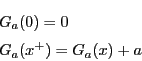
![]() よって,
よって,![]() と
と![]() の積
の積![]() を
を
この演算を乗法とする.乗法は可換であり単位元1をもつ.逆元はもたない.
加法と乗法に関して分配法則が成り立つ.つまり整数![]() は環である.
は環である.
この順序と演算に関して次の性質が成り立つ.
順序関係をもつので![]() は順序環といわれる.
は順序環といわれる.
証明
数
![]() に対して負でない数
に対して負でない数
![]() を
を
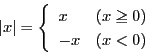
![]() に対して不等式
に対して不等式
その証明は次の補題による.
![]() とする.
とする.
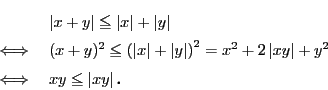
これを三角不等式という.三角不等式の成り立つ絶対値が定義されると,
これを用いて距離が定義される.つまり2数![]() と
と![]() の距離を
の距離を
![]() を整数の集合とする.次のような整数の組の集合を考える.
を整数の集合とする.次のような整数の組の集合を考える.
![]() の要素
の要素![]() に対し自然な形で和
に対し自然な形で和![]() と積
と積![]() が定まる.
こうして集合
が定まる.
こうして集合![]() は次のような量の要請をすべて満たしている.
は次のような量の要請をすべて満たしている.
まず全順序集合である.つまり![]() は全順序集合4である.
つまり,二つの有理数
は全順序集合4である.
つまり,二つの有理数
![]() に関して,
に関して,
そして![]() は体である.つまり二つの演算,
加法と乗法が定義され次の性質を満たす.
は体である.つまり二つの演算,
加法と乗法が定義され次の性質を満たす.
この順序と演算に関して整数と同様に 和および正数の積は順序を保存する. 以上を満たす構造をもつ集合を順序体という.
有理数の集合![]() は任意の要素
は任意の要素![]() に対して,
に対して,
実際,
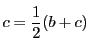 とおけば
とおけばこのような集合は稠密であるといわれる. こうして有理数は稠密な全順序体である.