集合![]() の要素
の要素![]() が集合
が集合![]() の要素
の要素![]() に対応するとき,これを
に対応するとき,これを![]() と書く.関数における
と書く.関数における![]() や
や![]() は個別の要素と考えることもできる.しかし,文字とはそもそもそこに「数を入れる箱」でもあるので,
は個別の要素と考えることもできる.しかし,文字とはそもそもそこに「数を入れる箱」でもあるので,![]() では箱
では箱 ![]() に集合
に集合![]() の要素を入れると,それに対応して
の要素を入れると,それに対応して![]() の要素が定まる.その値を入れる箱 が
の要素が定まる.その値を入れる箱 が ![]() であるとも考えることができる.
であるとも考えることができる.
例えば,![]() とする.
とする.![]() に
に![]() で対応する値が
で対応する値が![]() であると考えることができるが,また関数
であると考えることができるが,また関数![]() は
は
![]() の
の![]() に集合
に集合![]() の要素である値
の要素である値![]() を入れることで,集合
を入れることで,集合![]() の要素
の要素![]() が対応するという機能そのものを
が対応するという機能そのものを![]() で表しているとも考えることができる.
で表しているとも考えることができる.
関数の![]() に対し集合
に対し集合![]() を定義域,それに対し集合
を定義域,それに対し集合![]() の部分集合
の部分集合
関数は変数にどのような文字を使うかを明示して![]() と書くこともあれば,
と書くこともあれば,![]() と書くこともある.また
と書くこともある.また![]() のように書くこともある.同一の関数を適宜
のように書くこともある.同一の関数を適宜![]() と書いたり
と書いたり![]() と書いたりもする.
と書いたりもする.
関数というのは,数から数への対応の規則なので,一つの式で表される必要はない.例えば,
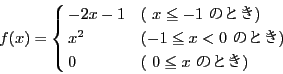
写像に関する,合成,全射・単射,逆写像の操作は,そのまま関数についてもあてはまる.また写像のグラフもまたそのまま関数のグラフに適用することができる.実数域で定義され,値域もまた実数である関数![]() において,
において,![]() 平面
平面![]() の部分集合
の部分集合
これを「整関数」ということがあるがこれは正しくない.後に述べるが,任意の閉区間で一様に収束する巾級数
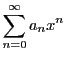 を「整関数」という.つまり,次数という点から見ると無限次数の多項式も含めて「整関数」である.また,複素関数論の分野になるのだが定義域を複素数にすると「整関数」は複素数を定義域とする関数で複素数全体で微分可能な関数と同等の意味になる.
を「整関数」という.つまり,次数という点から見ると無限次数の多項式も含めて「整関数」である.また,複素関数論の分野になるのだが定義域を複素数にすると「整関数」は複素数を定義域とする関数で複素数全体で微分可能な関数と同等の意味になる.
整式関数はもちろん整関数なのだけれど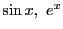 なども整関数である.高校の参考書で整式関数のことを整関数といっているものがあるが,数学全体で言葉は統一して使うべきである.
なども整関数である.高校の参考書で整式関数のことを整関数といっているものがあるが,数学全体で言葉は統一して使うべきである.
整式![]() と
と![]() を用いて
を用いて
![]() と書かれる式を有理式といい,
と書かれる式を有理式といい,![]() が有理式のとき関数
が有理式のとき関数![]() を有理関数という.また,整式
を有理関数という.また,整式![]() を用いて
を用いて
![]() と分数べきで書かれる部分をもつ式を無理式という.
と分数べきで書かれる部分をもつ式を無理式という.![]() が無理式とき関数
が無理式とき関数![]() を無理関数という.
を無理関数という.
三角関数,指数関数についてはいくつかの準備が必要なので,後に定義する.
数列の収束を有限の言葉で論述するために![]() 論法は不可欠であった.関数の連続性や収束性を論述するためにも
論法は不可欠であった.関数の連続性や収束性を論述するためにも
![]() 論法を用いる.連続性の厳密な定義そのものが
論法を用いる.連続性の厳密な定義そのものが
![]() 論法を必要としている.
論法を必要としている.
関数は実数の部分区間![]() で定義されたものとする.
で定義されたものとする.![]() は閉区間
は閉区間![]() ,開区間
,開区間![]() ,半開区間
,半開区間![]() ,
,![]() 等である.ただし,区間の端点が開いている場合,
等である.ただし,区間の端点が開いている場合,![]() としては
としては![]() ,
,![]() としては
としては![]() もあるものとし,
もあるものとし,
![]() ,半開区間
,半開区間![]() ,
,![]() 等も考えるものとする.
等も考えるものとする.
実数の区間![]() で定義され実数値をとる関数を
で定義され実数値をとる関数を![]() とする.
とする.![]() は集合
は集合![]() から実数の集合
から実数の集合![]() への写像に他ならない.以下
への写像に他ならない.以下![]() はこのような関数であるとする.
はこのような関数であるとする.
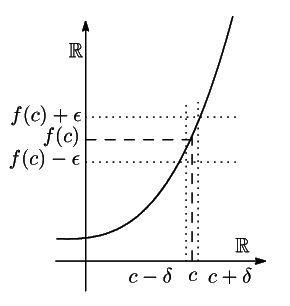 関数
関数次のように数列の収束性の問題としてとらえることもできる.
証明
逆を示す.定義の条件が成立しないとする.つまり正の実数![]() で次の条件がなり立つものが存在するとする.
で次の条件がなり立つものが存在するとする.
(1) 区間![]() の部分集合
の部分集合![]() を
を
同様に![]() なら,
なら,
![]() の
の![]() に対して
に対して![]() となりやはりこれは
となりやはりこれは![]() が
が![]() となる部分集合の上限であることに反する.
となる部分集合の上限であることに反する.
よって![]() である.
である.
![]() より
より![]() ,つまり
,つまり![]() である.
である.
(2)
![]() のとき.
のとき.
![]() とすると
とすると
![]() となり
となり![]() で
で![]() となるものが存在する.このとき
となるものが存在する.このとき![]() である.逆の場合も同様である.
□
である.逆の場合も同様である.
□
まず,次の補題を示す.
定理27の証明
![]() は
は![]() で有界であるから,
で有界であるから,
![]() を
を![]() の値域とするとき
の値域とするとき![]() は有界であり
は有界であり![]() の上限,下限が存在する.
の上限,下限が存在する.
![]() とする.
とする.
![]() となる
となる![]() の存在を示す.
の存在を示す.
![]() に属する
に属する![]() で
で
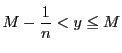 となるものが存在する.存在しないということは
となるものが存在する.存在しないということは![]() の要素
の要素![]() がすべて
がすべて
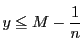 となるので,
となるので,![]() が上界の最小値であることに反するからである.このような
が上界の最小値であることに反するからである.このような![]() の一つを
の一つを![]() とする.数列
とする.数列
![]() は
は
![]() を満たす.
を満たす.
![]() は値域なので
は値域なので![]() となる
となる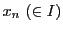 が存在する.数列
が存在する.数列![]() は有界であるから,定理19によって収束部分列が存在する.それを
は有界であるから,定理19によって収束部分列が存在する.それを
![]() とし
とし
![]() とする.
とする.![]() は閉区間であるから
は閉区間であるから![]() である.
である.![]() は
は![]() で連続なので
で連続なので
最小値![]() を与える
を与える![]() の値の存在も同様に示される.
□
の値の存在も同様に示される.
□
これら二つの存在定理は高校解析では「知られている」こととして提示される.そしてそれを根拠に「ロルの定理」,「平均値の定理」を証明する.二つの存在定理自体の証明は実数論をもとに大学初年級の数学でおこなう.
高校数学での中間値の定理などを,存在定理を感覚的な理解に留めるのではなく,高校,大学の役割分担を明示して,一貫した体系で教えなければならない.そのために,高校生に数学を教えるものは,その全体をつかみ,必要に応じて生徒に問いかけ,また答えることができなければならない.
もちろん,数学の歴史でもはじめから実数について今日のような理解があったわけではない.長い歴史のうえに今日があることを追体験したいものである.