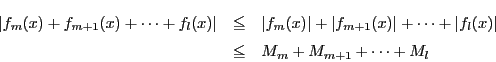次: 初等関数
上: 関数の概念
前: 連続関数
次: 初等関数
上: 関数の概念
前: 連続関数
解析の基礎において重要な問題は実は「一様連続」といわれる概念である. 高校の級数の収束や積分の定義などあらゆるところで現れている.しかし明示的には示されない.そこでこれを取り出して定義しておきたい.歴史的には,一様連続性の概念をつかむことによって,解析学の基礎が飛躍的に深まった.なお「一様連続性」とは「一様連続」が成立する関数のある性質,の意味である.
定義 15 (関数の一様連続性)
区間 で定義された関数
で定義された関数 がある.任意の正の実数
がある.任意の正の実数 に対して,正の実数
に対して,正の実数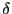 で
で
となるものが存在するとき,関数

は区間

で一様連続である,という.
■
一様連続でない例を考えるとよくわかる.区間 が閉区間なら,
が閉区間なら, で連続なら
で連続なら で一様連続になることが次に示される.したがって開区間を考えなければならない.
で一様連続になることが次に示される.したがって開区間を考えなければならない.
例 3.3
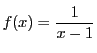
は区間
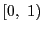
で一様連続ではない.
証明
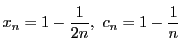 とすると
とすると
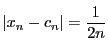 であるが
であるが
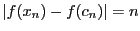 である.したがって与えられた
である.したがって与えられた に対しどのように
に対しどのように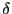 をとっても
をとっても を大きくとれば
を大きくとれば
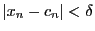 であるが
であるが
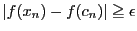 となる
となる と
と が存在し,一様連続の条件はみたさない.
□
が存在し,一様連続の条件はみたさない.
□
これは, が1に近づくと
が1に近づくと が少し動いても
が少し動いても が大きく動くことになり,区間によらない
が大きく動くことになり,区間によらない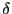 がとれないのである.
がとれないのである.
閉区間ではこのようなことは起こらない.
定理 28
閉区間

で連続な関数

は

で一様連続である.
■
証明
背理法で示す. について一様連続の条件が成立しないとする.ある
について一様連続の条件が成立しないとする.ある をとるとすべての
をとるとすべての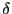 に対しある
に対しある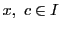 が存在して,
が存在して,
となる.
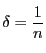 とし,
とし, と
と を
を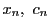 とする.数列
とする.数列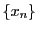 は有界数列なので,定理19によって収束部分列
は有界数列なので,定理19によって収束部分列
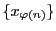 が存在する.その極限値を
が存在する.その極限値を とする.
とする.
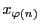 に対応する
に対応する
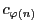 からなる数列も,
からなる数列も,
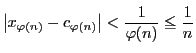 であるから同じ
であるから同じ に収束する.
に収束する. は閉区間なので
は閉区間なので は
は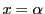 で連続である.よって
で連続である.よって
これは,
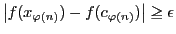 と矛盾する.
と矛盾する.
ゆえに閉区間 で連続な関数
で連続な関数 は
は で一様連続であることが示された.
□
で一様連続であることが示された.
□
関数列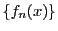 とは自然数を添え字とする関数の集合である.
とは自然数を添え字とする関数の集合である.
関数 と関数列
と関数列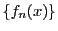 がある.
がある. を固定したとき
を固定したとき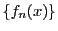 は一つの数列である.
は一つの数列である. が一定の区間にあるとき,動くのは
が一定の区間にあるとき,動くのは と
と である.ここで,収束関数列の一様収束性の概念が生まれる.これについて基礎的事項を示していこう.
である.ここで,収束関数列の一様収束性の概念が生まれる.これについて基礎的事項を示していこう.
定義 16 (関数列の一様収束)
区間

で定義された関数

と同じ区間で定義された関数の列
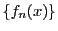
がある.任意の正数

が与えられたとき,

に属する任意の

に対して,

によらない自然数

で,
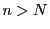
ならば
となるものが存在するとき,関数列
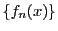
は関数

に一様収束するという.
■
定理 29
区間

で定義された関数

と同じ区間で定義された関数の列
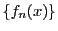
がある.関数列
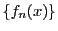
は関数

に一様収束し,すべての自然数

に対して
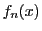
が

で連続なら,

も

で連続である.
■
証明
任意の正数 が与えられたとき,
が与えられたとき, に属する
に属する に対して,
に対して, によらない自然数
によらない自然数 で,
で,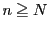 ならば
ならば
となるものが存在する.また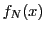 は連続なので,区間
は連続なので,区間 の任意の
の任意の に対し,正数
に対し,正数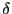 で,
で,
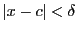 ならば
ならば
となるものが存在する.このとき
ゆえに は
は で連続である.
□
で連続である.
□
数列の基本数列,あるいはコーシー数列といわれる収束数列の概念と同様に,関数列に対してもコーシー列が定義される.
定義 17 (コーシー関数列)
区間

で定義された関数の列
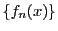
がある.任意の正数

が与えられたとき,

に属する任意の

に対して,

によらない自然数

で,
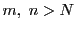
ならば
となるものが存在するとき,関数列
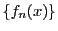
は
コーシー関数列であるという.
■
定理 30
区間

で定義された関数列
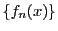
がコーシー関数列であれば,関数列
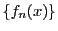
は

を定義域とするある関数

に一様収束する.
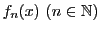
が連続なら

も連続である.
■
証明
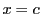 を固定すると関数値の数列
を固定すると関数値の数列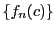 はコーシー数列である.実数の完備性によってある実数値に収束する.その値を
はコーシー数列である.実数の完備性によってある実数値に収束する.その値を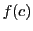 とする.
とする.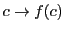 によって関数
によって関数 が定まり
が定まり を固定するごとに収束する.ところが
を固定するごとに収束する.ところが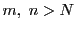 ならば
ならば
となる が存在するので,この両辺を
が存在するので,この両辺を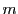 の数列と見て
の数列と見て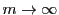 とすると,
とすると,
が得られ, は
は によらないので,関数列
によらないので,関数列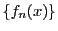 は関数
は関数 に一様収束する.連続性に関する命題は定理30より従う.
■
に一様収束する.連続性に関する命題は定理30より従う.
■
関数を項とする級数
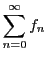 についても,実数を項とする級数と同様に,部分和
についても,実数を項とする級数と同様に,部分和
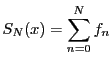 によって定まる関数列
によって定まる関数列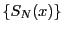 の極限として定義される.関数列
の極限として定義される.関数列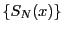 が
が に一様収束するとき,級数
に一様収束するとき,級数
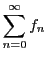 は
は に一様収束するという.
に一様収束するという. をその和といい,
をその和といい,
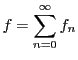 と表す.
と表す.
定理 31

で定義された関数列
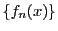
からできる級数
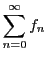
が一様収束するための必要十分条件は,任意の正数

が与えられたとき,
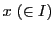
によらない番号

で,
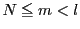
ならば
となるものが存在することである.
■
証明
これは定理21からただちに従う.
□
系 31.1
正項級数
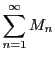
が収束し,区間

で定義された関数
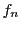
を項とする級数
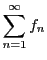
について
が成立すれば,
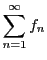
,
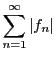
は一様収束し,和について
が成り立つ.
■
証明
 の
の について
について
が成り立つ.
定理31から従う.
□
これらの定理は後に関数の級数展開,微分方程式の解の存在定理を論じる基礎になる.


 次: 初等関数
上: 関数の概念
前: 連続関数
次: 初等関数
上: 関数の概念
前: 連続関数
2014-05-23
![]() で定義された関数
で定義された関数![]() がある.任意の正の実数
がある.任意の正の実数![]() に対して,正の実数
に対して,正の実数![]() で
で
![]() が閉区間なら,
が閉区間なら,![]() で連続なら
で連続なら![]() で一様連続になることが次に示される.したがって開区間を考えなければならない.
で一様連続になることが次に示される.したがって開区間を考えなければならない.
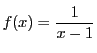 は区間
は区間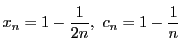 とすると
とすると
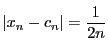 であるが
であるが
![]() が1に近づくと
が1に近づくと![]() が少し動いても
が少し動いても![]() が大きく動くことになり,区間によらない
が大きく動くことになり,区間によらない![]() がとれないのである.
がとれないのである.
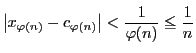 であるから同じ
であるから同じ![]() で連続な関数
で連続な関数![]() は
は![]() で一様連続であることが示された.
□
で一様連続であることが示された.
□
![]() と関数列
と関数列![]() がある.
がある.![]() を固定したとき
を固定したとき![]() は一つの数列である.
は一つの数列である.![]() が一定の区間にあるとき,動くのは
が一定の区間にあるとき,動くのは![]() と
と![]() である.ここで,収束関数列の一様収束性の概念が生まれる.これについて基礎的事項を示していこう.
である.ここで,収束関数列の一様収束性の概念が生まれる.これについて基礎的事項を示していこう.
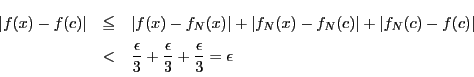
![]() についても,実数を項とする級数と同様に,部分和
についても,実数を項とする級数と同様に,部分和
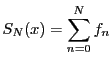 によって定まる関数列
によって定まる関数列![]() の極限として定義される.関数列
の極限として定義される.関数列![]() が
が![]() に一様収束するとき,級数
に一様収束するとき,級数
![]() は
は![]() に一様収束するという.
に一様収束するという.![]() をその和といい,
をその和といい,
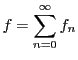 と表す.
と表す.