しかしこの値は平均化されたものである.車の速度計は刻々変化する.自由落下では重力による加速度によって速度は増加する.このように日常的には平均化された値が使われ(それは一次近似なのだが)るが,実際は,はかる時点や場所によって変化する局所的な量である.
濃度は,100g の塩水に 10g の塩が含まれている場合,これを濃度 0.1 という.しかしこれは濃さが均質なときであって,塩の分布が一様でなければ,塩水の位置によって濃度は変化する.ある点の近くでのことが全体に広がっていると仮定して濃いとか辛いとかいってい.つまり,濃度は本来局所的な量である.一様でないとき,0.1 という数は,平均の濃度を表す.ただし,それは口に入れた点でのことで,それが均質に一様に広がっているかどうかはわからない.一様でない場合,どのように考えてゆけばよいのか.
このような考察が,関数概念の獲得と一体になって,平均変化率,そして微分へと進んだのはまちがいないであろう.
現実を近似し解析するために実数を準備した.これによって現実の諸関係が関数によって表現された.さらに現実の物理現象など深く解析するために,関数![]() の解析方法を準備しなければならない.もちろん濃度のように,空間の位置を表すために三つの実数が必要なこともある.また速度も方向まで考えれば少なくとも2次元のベクトルで考えなければならない.つまり,
の解析方法を準備しなければならない.もちろん濃度のように,空間の位置を表すために三つの実数が必要なこともある.また速度も方向まで考えれば少なくとも2次元のベクトルで考えなければならない.つまり,![]() や
や![]() を多元量としてとらえなければならない.
を多元量としてとらえなければならない.
最も簡単で基礎的なのが量が一つの実数に対応する一次元の場合である.まず二つの実数![]() と
と![]() のあいだの関数
のあいだの関数![]() について考える.一変数の量となる例は,時間と位置の関係,その変化の比としての速度などであるが,そのような具体的な量を念頭におきながらも,実数の関数の問題として考える.こうして後に現実の量を解析するための方法を準備する.
について考える.一変数の量となる例は,時間と位置の関係,その変化の比としての速度などであるが,そのような具体的な量を念頭におきながらも,実数の関数の問題として考える.こうして後に現実の量を解析するための方法を準備する.
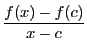 に対し,極限値
に対し,極限値
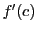 と表す.
■
と表す.
■
![]() とおく.
とおく.![]() なので
なので![]() のとき
のとき![]() である.微分係数を次式の極限値の存在で定義してもよい.
である.微分係数を次式の極限値の存在で定義してもよい.
関数![]() からその導関数
からその導関数![]() を求めることを関数
を求めることを関数![]() を微分するという.
■
を微分するという.
■
関数![]() の導関数
の導関数![]() を表す記号はさまざまに用いられてきた.関数
を表す記号はさまざまに用いられてきた.関数![]() の導関数
の導関数![]() のように変数を書かないこともある.
のように変数を書かないこともある.![]() は
は
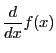 とも表す.さらに関数
とも表す.さらに関数![]() と
と![]() が定まっているときは,
が定まっているときは,![]() や
や
![]() などのようにも表す.
などのようにも表す.![]() はニュートンに由来する記号であるが近年は余り用いない.いずれにせよ次の記号はそれぞれの歴史があり,また記号のかたちの意味づけもできるが,導関数を定義した段階では同じものを表すとしてよい.
はニュートンに由来する記号であるが近年は余り用いない.いずれにせよ次の記号はそれぞれの歴史があり,また記号のかたちの意味づけもできるが,導関数を定義した段階では同じものを表すとしてよい.
$ c $ で連続で, \[ f(x)=f(c)+(x-c)\phi(x) \] となる関数 $ \phi(x) $ が存在する.このとき,$ f'(c)=\phi(c) $ である. ■
$ f(x) $ が $ x=c $ で微分可能であるとする. ここで関数 $ \phi(x) $ を次のように定義する. \[ \phi(x)= \left\{ \begin{array}{ll} \dfrac{f(x)-f(c)}{x-c}&(x\ne c)\\ f'(c)&(x=c) \end{array} \right. \] $ f(x) $が $ x=c $ で微分可能なので, \[ \lim_{x \to c}\phi(x)=f'(c)=\phi(c) \] となり,$ \phi(x) $ は $ x=c $ で連続である.そして,定理の関係式を満たす.
定理の $ \phi(x) $ が存在するとする. $ x\ne c $ のとき \[ \dfrac{f(x)-f(c)}{x-c}=\phi(x) \] で, $ \phi(x) $ の連続性から \[ \lim_{x \to c}\phi(x)=\lim_{x \to c}\dfrac{f(x)-f(c)}{x-c} \] が存在し,$ f(x) $ は $ x=c $ で微分可能である. □
証明
(1)
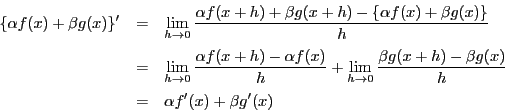
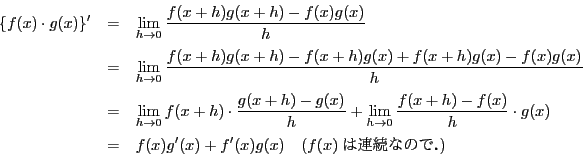
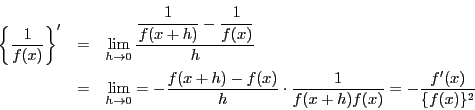
注意
定理※を用いれば,本定理の証明は,もう少し簡明になる.
しかし,上記証明の変形も意味あるので,高校数学範囲の証明にした.
それに対して,合成関数の微分の関する次定理は2通りの証明を行う.
第1法は高校教科書の方法であるが,例えば,関数 $g(x)$ が定数のとき $g(x+h)-g(x)=0$ となり,
このままでは該当の変形ができない.
ここは歴史的にもいろいろ工夫されてきたところであり,第2法はこの場合を含めて,可能な証明である.
証明
(4)
第1法
実数![]() に対して
に対して
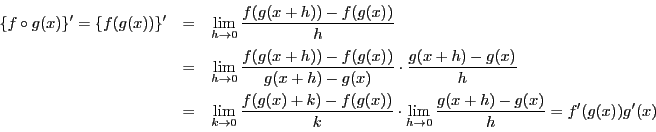
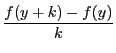 が0でない
が0でない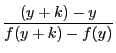 も0でない有限値
も0でない有限値
関数![]() と
と![]() の合成は,変数を区別して
の合成は,変数を区別して
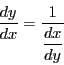
このように![]() が微分可能であれば
が微分可能であれば![]() は連続であるが,逆は成り立たない.
は連続であるが,逆は成り立たない.![]() は実数全体で連続であるが,
は実数全体で連続であるが,![]() で微分可能ではない.
で微分可能ではない.
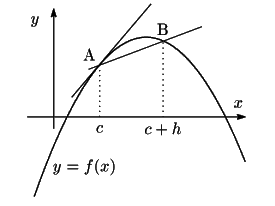 関数
関数
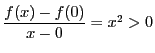 であるが,
であるが,
逆に区間において微分可能で![]() が成り立つとき,
が成り立つとき,
![]() はこの区間で単調増加している.
これを証明するためには平均値が必要である.
平均値の定理の系として示す.
はこの区間で単調増加している.
これを証明するためには平均値が必要である.
平均値の定理の系として示す.
以上の議論は関数の減少についても同様である.
![]() が成り立つとき極小であるという.
■
が成り立つとき極小であるという.
■
![]() は
は![]() で極小である.この場合のように微分できない点でも,
極大や極小であり得る.それに対して,
で極小である.この場合のように微分できない点でも,
極大や極小であり得る.それに対して,
![]() が微分可能な場合に
が微分可能な場合に![]() が
が![]() で極大であることは
で極大であることは
ことと同値である.で
は
の前後で正から負に変わる.