

 次: 関数解析
上: 微分の方法
前: 微分可能
次: 関数解析
上: 微分の方法
前: 微分可能
 が定数関数なら
が定数関数なら
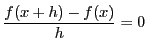 なので
なので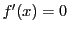 .
.
 が整式のとき.
が整式のとき. は定数と
は定数と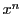 を定数倍したものの和なので,
を定数倍したものの和なので,
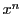 の微分ができれば,
の微分ができれば, の微分もできる.
の微分もできる.
 を自然数とする.
を自然数とする.
 の
の 乗である
乗である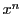 を微分する方法は3つある.
を微分する方法は3つある.
方法1
となることを,次数 に関する数学的帰納法で示す.
に関する数学的帰納法で示す.
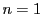 のときは明らかに成立.
のときは明らかに成立.
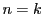 で成立とする.
このとき
で成立とする.
このとき
なので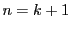 でも成立し,すべての
でも成立し,すべての で成立する.
で成立する.
方法2
直接示す方法の一つは二項定理を用いる.
二項定理とは,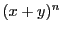 の展開式が
組合せの場合の数を表す記号
の展開式が
組合せの場合の数を表す記号
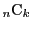 を用いて
を用いて
と表されることをいう.
これを用いて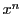 を微分しよう.
を微分しよう.
方法3
もう一つは,因数分解
を用いる方法である.この因数分解で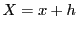 ,
,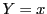 とすると
とすると
なので
ここで
なので,これから
となる.
□
有理数 に対して
に対して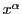 の微分は指数関数と対数関数の微分からも求まる.
が,直接求めることもできる.以下
の微分は指数関数と対数関数の微分からも求まる.
が,直接求めることもできる.以下 は自然数とする.
は自然数とする.
商の微分から
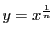 は,
区間
は,
区間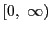 で単調増加な関数
で単調増加な関数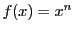 の逆関数である.
逆関数の微分から
の逆関数である.
逆関数の微分から
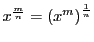 なので
2つの関数
なので
2つの関数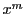 と
と
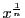 の合成関数である.
合成関数の微分から
の合成関数である.
合成関数の微分から
なので
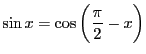 より
より
また
逆三角関数の定義3.4にしたがってそれぞれの定義域に注意する.
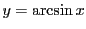 とする.
とする.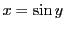 より
より
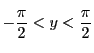 範囲の
範囲の に対して
に対して
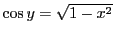 である.
である.
同様に
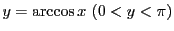 とする.
とする.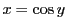 よりこの範囲の
よりこの範囲の に対して
に対して
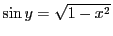 である.
である.
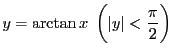 とする.
とする.
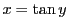 よりこの範囲の
よりこの範囲の に対して
に対して
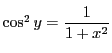 である.
である.
1章2節の系33.1より
なので
である.
また1でない正数 に対して
に対して
ここで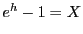 とおく.
とおく.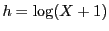 である.
である.
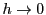 のとき
のとき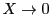 なので
なので
よって
また1でない正数 に対して
に対して
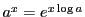 であるから
であるから
ここで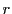 は任意の実数,定義域は
は任意の実数,定義域は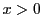 とする.
とする.
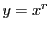 とする.
とする.
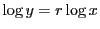 の両辺を
の両辺を で微分する.
で微分する.
これから
このように対数をとって微分する方法を対数微分という.


 次: 関数解析
上: 微分の方法
前: 微分可能
次: 関数解析
上: 微分の方法
前: 微分可能
2014-05-23
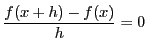 なので
なので![]() の展開式が
組合せの場合の数を表す記号
の展開式が
組合せの場合の数を表す記号
![]() を用いて
を用いて
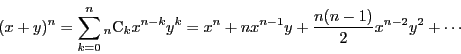
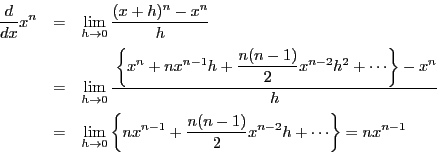
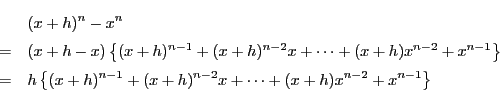
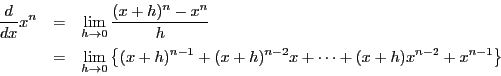
![]() に対して
に対して![]() の微分は指数関数と対数関数の微分からも求まる.
が,直接求めることもできる.以下
の微分は指数関数と対数関数の微分からも求まる.
が,直接求めることもできる.以下![]() は自然数とする.
は自然数とする.
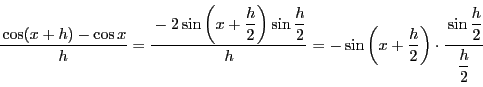
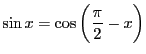 より
より
![]() とする.
とする.![]() より
より
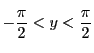 範囲の
範囲の![]() に対して
に対して
![]() である.
である.
![]() とする.
とする.![]() よりこの範囲の
よりこの範囲の![]() に対して
に対して
![]() である.
である.
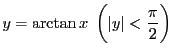 とする.
とする.
![]() よりこの範囲の
よりこの範囲の![]() に対して
に対して
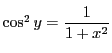 である.
である.