![]() をある与えられた集合とし,
をある与えられた集合とし,
![]() を
を![]() から
から![]() への写像とする.
への写像とする.
![]() の要素で
の要素で![]() となるものを
となるものを![]() の不動点という.
の不動点という.
証明
![]() である.
である.
![]() なら
なら![]() が,
が,![]() なら
なら![]() が不動点である.
が不動点である.
![]() とする.
とする.
![]() なので
連続関数
なので
連続関数![]() に関する中間値の定理によって,
に関する中間値の定理によって,
![]() となる
となる![]() が存在する.
が存在する.
![]() が
が![]() の不動点である.
□
の不動点である.
□
次の例は大学入試(92神戸大)で出題された.
証明
![]() である.
である.
![]() なら
なら ![]() として
として![]() をとればよい.
をとればよい.
![]() なら
なら ![]() として
として![]() をとればよい.そこで
をとればよい.そこで![]() とする.
とする.
このとき,![]() かつ
かつ ![]() なので
なので ![]() となる
となる ![]() の中の最大のものが存在する.それを
の中の最大のものが存在する.それを ![]() とする.
とする.![]() である.
である.
![]() は
は ![]() を満たさないので
を満たさないので
![]() .
ところが
.
ところが![]() ならば,つねに
ならば,つねに![]() なので
なので
縮小写像の条件から,縮小写像は連続である.
証明
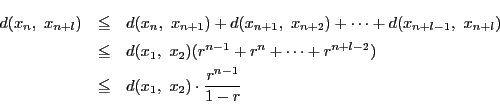
![]() となる点があるとする.
となる点があるとする.
から
この定理は単純であるが,大変有用である. 積分方程式や微分方程式の解の存在, およびその解に収束する関数列の構成に応用することができる.
縮小写像より一般的な連続写像に関する不動点定理は位相幾何学の分野である. 例えば次のような定理が成り立つ.
![]() のときが例6.2である.
一般的な証明は位相幾何学の準備がいる.
例えば文献『位相幾何学』[25]のような位相幾何学の入門書を見てほしい.
ここでは文献『直観幾何学』[25]によって,
のときが例6.2である.
一般的な証明は位相幾何学の準備がいる.
例えば文献『位相幾何学』[25]のような位相幾何学の入門書を見てほしい.
ここでは文献『直観幾何学』[25]によって,![]() つまり円板の場合にこれを証明しよう.
つまり円板の場合にこれを証明しよう.
![]() のときの証明
のときの証明
円板![]() 上に
上に![]() の不動点が存在しないと仮定し矛盾が起こることを示す.
の不動点が存在しないと仮定し矛盾が起こることを示す.
![]() を中心を原点にして
を中心を原点にして![]() 平面に置く.
平面に置く.![]() は不等式
は不等式![]() で表される.
で表される.
![]() に対し円
に対し円![]() を
を![]() とする.
とする.
![]() の任意の点
の任意の点![]() に対し
に対し
![]() なので,
ベクトル
なので,
ベクトル
![]() をとることができる.
をとることができる.
![]() が連続なのでこのベクトルの大きさも向きも連続的に変化する.
が連続なのでこのベクトルの大きさも向きも連続的に変化する.
ベクトル
![]() が
が![]() 軸の正の方向となす角を
軸の正の方向となす角を
![]() とし,
点
とし,
点![]() を
を![]() 上反時計回りに一周させたときの
変化量を
上反時計回りに一周させたときの
変化量を![]() とする.
とする.
![]() とおく.
一周すれば元に戻るのだから
とおく.
一周すれば元に戻るのだから![]() は
は![]() の整数倍である.
の整数倍である.
![]() を求める.
点
を求める.
点![]() での円
での円![]() の接線ベクトルのうち,
ベクトル
の接線ベクトルのうち,
ベクトル
![]() を
左側に見るものが
を
左側に見るものが![]() 軸の正の方向となす角を
軸の正の方向となす角を![]() とする.
最初点
とする.
最初点![]() を
を![]() 上の
上の![]() にとる.
このとき
にとる.
このとき
![]() である.
である.
![]() を反時計回りに一周する.
を反時計回りに一周する.
![]() は0から
は0から![]() まで変化する.
まで変化する.
仮に![]() の変化量
の変化量![]() が
が![]() でないと仮定する.
すると1周まわったとき角
でないと仮定する.
すると1周まわったとき角![]() は
は![]() 以上か0以下である.
2つの角の差
以上か0以下である.
2つの角の差![]() は,最初
は,最初
![]() にあり,
一周して点
にあり,
一周して点![]() が
が![]() に戻ったとき,
に戻ったとき,
![]() である.
である.
![]() は連続的に変化するので,途中で
は連続的に変化するので,途中で
![]() となるか
となるか
![]() となるときがある.
一方,
となるときがある.
一方,![]() が
が![]() の周か内部にあり
の周か内部にあり
![]() にあるので
にあるので
![]() である.矛盾が起こる.
つまり
である.矛盾が起こる.
つまり![]() である.
である.
![]() の変化に対して角
の変化に対して角![]() は連続的に変化するので
は連続的に変化するので![]() も連続的に変化する.
ところが
も連続的に変化する.
ところが![]() は
は![]() の整数倍しかとり得ないので,すべての
の整数倍しかとり得ないので,すべての![]() に対して
に対して
![]() である.
である.
しかし![]() のとき
のとき
![]() であり,
であり,
![]() の連続性から角
の連続性から角![]() の変化量も0に収束する.
これは矛盾である.
従って
の変化量も0に収束する.
これは矛盾である.
従って![]() は不動点をもつ.
□
は不動点をもつ.
□
位相幾何,あるいは函数解析といわれる広大な分野に近づいてきているが, ここで踵を返し,多次元の微積に戻らなければならない.