

 次: 面積速度
上: 惑星の運動
前: 物理法則
次: 面積速度
上: 惑星の運動
前: 物理法則
そこで,ニュートンの法則と万有引力の法則を結びつける.
太陽と地球の間の運動は,いわゆる二体問題である.
だから太陽と地球全体の重心を問題にしなければならない.
しかし,太陽の質量は地球に比べてはるかに大きい.
したがって,太陽と地球全体の重心は,太陽に一致するとしてよい.
その結果,太陽は動かず地球が太陽の周りを動くとして考えてよい.
次に太陽も地球も巨大な物体である.
しかし剛体の運動はその重心に質量がある点の運動と考えることが出来る.
太陽の質量を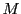 ,地球の質量を
,地球の質量を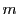 ,万有引力定数を
,万有引力定数を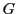 とする.
太陽を基準点とする地球の位置をベクトル
とする.
太陽を基準点とする地球の位置をベクトル
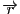 で表す.
時を
で表す.
時を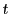 で表す.
するとニュートンの法則と万有引力の法則から
で表す.
するとニュートンの法則と万有引力の法則から
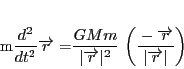 |
(11) |
が成立する.最後の
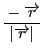 は地球から
太陽に向かう方向の単位ベクトルで,つまりは引力の方向を表す大きさ1のベクトルである.
は地球から
太陽に向かう方向の単位ベクトルで,つまりは引力の方向を表す大きさ1のベクトルである.
等式11はベクトル成分の微分方程式である.
多次元の微積で準備したことと微分方程式で準備したことをもとに,
この微分方程式11からケプラーの法則を導きだそう.
いま考えているベクトルは空間ベクトルであるが,
しかし次のことを示せば,あとは平面ベクトルだけを考えればよい.
ここで中心力とは,二つの質点の間で二つの質点を結ぶ直線方向に働く力のことである.
定理 87
記号の意味は微分方程式
11と同様とする.
太陽と地球の間に中心力のみが働いている場合,
つまり
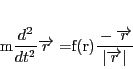 |
(12) |
とかける場合,地球は一つの平面上を運動する.
■
証明の準備をする.
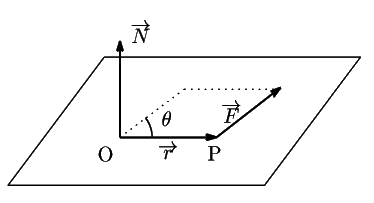 図のように, 力
図のように, 力
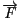 が位置ベクトル
が位置ベクトル
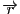 の質点
の質点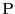 に作用するとき,
ベクトル
に作用するとき,
ベクトル
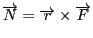 を
力
を
力
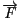 の基準点
の基準点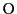 の周りにもつモーメントという.
の周りにもつモーメントという.
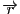 と
と
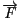 のなす角を
のなす角を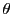 とすると,
ベクトル
とすると,
ベクトル
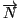 の大きさは
の大きさは
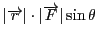 である.
である.
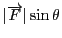 はちょうど力
はちょうど力
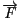 の
の
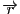 と直交する方向の大きさになるので,
力のモーメントの大きさは点
と直交する方向の大きさになるので,
力のモーメントの大きさは点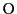 の周りの回転させる力の強さを表す.
の周りの回転させる力の強さを表す.
一般に,
質点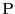 にある物理量
にある物理量
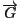 と
基準点
と
基準点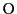 に関する
に関する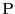 の位置ベクトル
の位置ベクトル
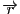 に対して,
外積
に対して,
外積
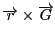 を
を
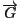 が点
が点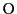 の周りにもつモーメントという.
の周りにもつモーメントという.
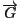 が運動量
が運動量
であるとき,この運動量
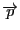 のモーメント
のモーメント
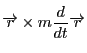 を角運動量という.
を角運動量という.
等式12の両辺のモーメントをとる.
左から
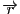 を外積でかける.
を外積でかける.
右辺は
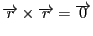 より
より
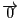 である.
左辺において定数以外の部分を変形すると
である.
左辺において定数以外の部分を変形すると
である.したがって
つまり,
が成り立つ.
運動量ベクトルは
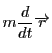 なので
これはまさに角運動量が時間に対して一定であることを示している.
なので
これはまさに角運動量が時間に対して一定であることを示している.
一方,
これは二つのベクトル
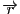 と
と
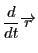 がつねに
がつねに
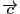 と直交していることを示す.
運動は時間に関して連続的であるから,
二つのベクトル
と直交していることを示す.
運動は時間に関して連続的であるから,
二つのベクトル
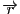 と
と
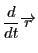 が
つねに同一の平面上にあることが示された.
□
が
つねに同一の平面上にあることが示された.
□
2014-05-23
![]() ,地球の質量を
,地球の質量を![]() ,万有引力定数を
,万有引力定数を![]() とする.
太陽を基準点とする地球の位置をベクトル
とする.
太陽を基準点とする地球の位置をベクトル
![]() で表す.
時を
で表す.
時を![]() で表す.
するとニュートンの法則と万有引力の法則から
で表す.
するとニュートンの法則と万有引力の法則から
 図のように, 力
図のように, 力
![]() が運動量
が運動量
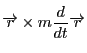 を角運動量という.
を角運動量という.
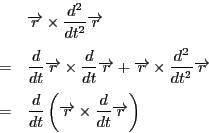
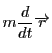 なので
これはまさに角運動量が時間に対して一定であることを示している.
なので
これはまさに角運動量が時間に対して一定であることを示している.
![]() と
と
![]() がつねに
がつねに
![]() と直交していることを示す.
運動は時間に関して連続的であるから,
二つのベクトル
と直交していることを示す.
運動は時間に関して連続的であるから,
二つのベクトル
![]() と
と
![]() が
つねに同一の平面上にあることが示された.
□
が
つねに同一の平面上にあることが示された.
□