

 次: 参考文献
上: 惑星の運動
前: 面積速度
次: 参考文献
上: 惑星の運動
前: 面積速度
さてわれわれの得た微分方程式をもとに,
惑星の軌道が楕円であることを導こう.
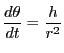 なので整理すると
なので整理すると
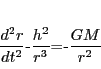 |
(14) |
となる.
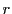 は質点間の距離であるが,距離,速度,加速度,といった数学的な量に対して,
位置エネルギー(本当は「ポテンシャル」というべき所だ),運動量,力,
といった物理学的な量が,特にそれが保存量である場合に,基本的な量である.
は質点間の距離であるが,距離,速度,加速度,といった数学的な量に対して,
位置エネルギー(本当は「ポテンシャル」というべき所だ),運動量,力,
といった物理学的な量が,特にそれが保存量である場合に,基本的な量である.
二つの質量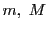 をもつ質点が万有引力で引き合い,距離
をもつ質点が万有引力で引き合い,距離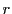 のときそれぞれ
速度が
のときそれぞれ
速度が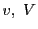 となったとする.万有引力による位置エネルギー
となったとする.万有引力による位置エネルギー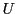 は
は
で定まる.これはエネルギー保存則
である.
この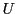 は,中心力が働く場でのポテンシャルといわれる.
ポテンシャルは
は,中心力が働く場でのポテンシャルといわれる.
ポテンシャルは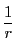 に比例している.
に比例している.
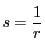 と変数を変換する.
と変数を変換する.
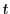 での微分を作ったうえで,
での微分を作ったうえで,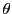 での微分に置きかえていく.
での微分に置きかえていく.
よって
となる.これから
が得られる.
つまり
ここで
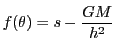 とおくと,
とおくと,
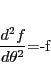 |
(15) |
となった.
この微分方程式を解けばよい.
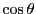 と
と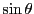 はともに二階微分方程式15
を満たし,そのロンスキアンは
はともに二階微分方程式15
を満たし,そのロンスキアンは
である.よって15の解はすべて
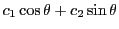 とかける.
これは合成すると
とかける.
これは合成すると
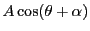 となる.角
となる.角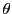 の始点をとりなおすことで
の始点をとりなおすことで
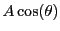 としてよい.
としてよい.
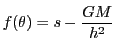 であったから
であったから
となる.
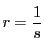 より
より
となった.
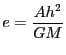 ,
,
 とおくと
とおくと
これは確かに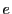 を離心率とする二次曲線である.
実際に惑星の軌道は閉じているのでこれは楕円でなければならない.
これがケプラーの第一法則である.
もちろん彗星などでは放物線になることもある.
を離心率とする二次曲線である.
実際に惑星の軌道は閉じているのでこれは楕円でなければならない.
これがケプラーの第一法則である.
もちろん彗星などでは放物線になることもある.
軌道が楕円であることが確定すれば,ケプラーの第三法則は数学の問題である.
この楕円の長軸は
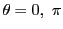 での
での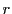 の和だから
の和だから
また短軸は
ゆえに
つまり
面積速度は
なので,周期を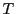 とすると楕円の面積は
とすると楕円の面積は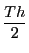 である.
である.
一方,面積は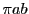 でもあるので
でもあるので
つまり「惑星の公転周期の2乗は軌道の半長径の3乗に比例する」というケプラーの第三法則が示された.


 次: 参考文献
上: 惑星の運動
前: 面積速度
次: 参考文献
上: 惑星の運動
前: 面積速度
2014-05-23
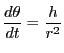 なので整理すると
なので整理すると
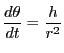 なので整理すると
なので整理すると
![]() は質点間の距離であるが,距離,速度,加速度,といった数学的な量に対して,
位置エネルギー(本当は「ポテンシャル」というべき所だ),運動量,力,
といった物理学的な量が,特にそれが保存量である場合に,基本的な量である.
は質点間の距離であるが,距離,速度,加速度,といった数学的な量に対して,
位置エネルギー(本当は「ポテンシャル」というべき所だ),運動量,力,
といった物理学的な量が,特にそれが保存量である場合に,基本的な量である.
![]() をもつ質点が万有引力で引き合い,距離
をもつ質点が万有引力で引き合い,距離![]() のときそれぞれ
速度が
のときそれぞれ
速度が![]() となったとする.万有引力による位置エネルギー
となったとする.万有引力による位置エネルギー![]() は
は
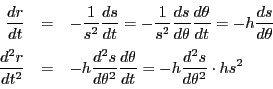
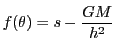 とおくと,
とおくと,
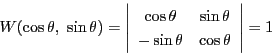
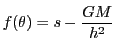 であったから
であったから
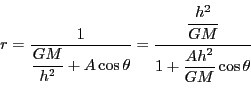
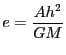 ,
,
 とおくと
とおくと
![]() での
での![]() の和だから
の和だから
![]() でもあるので
でもあるので