次: 集合と公理 上: まえがき 前: 人間を育てる

本稿の構成

$\epsilon -\delta$論法の意義

本稿では，数列と関数の収束に関する，いわゆる 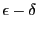$\epsilon -\delta$論法は終始一貫して用いる．この論法は，収束性を「すべて」と「存在する」という論理の言葉で論じる方法である．いわば無限を有限の言葉でつかむ方法である．数学的な現象を人間が論理の言葉でつかむうえで不可欠である．

もとより，この論法が確立するまでには幾多の試行錯誤があった．その歴史は『 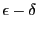$\epsilon -\delta$論法とその形成』[25]に詳しい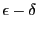． $\epsilon -\delta$論法もまた，歴史的制約の中での理論であり，それを最終的な方法であると言うことはできない．しかし，まずこの方法を習得し身につけることが，現代において数学を学ぶことことの意味の一つであり，この段階をふまえることは不可避である．

大学初年級の解析学ではここで躓くことが多いと言われる．この論法が苦手な人は，いちどこれを用いずに収束性を厳密に論じてみようとすればよい．やってみればただちに 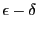$\epsilon -\delta$論法の重要性がわかる．まず自分で厳密な組み立てようとする．そして，やはり有限の言葉でこれをつかもうとすれば，これしかないことを納得する．この過程を経験することによってはじめてこの論法の重要性がわかり，日常的な言語感覚や論証感覚を省みることができる．

章立て

次のような内容を骨子に，いくつか関連したことを含めて展開するようにしたい．

第一，

現代数学は集合をその言葉として用いる．まずこれを整理するとともに，整列集合と選択公理についてのべる．その上で，整数の公理系を出発点とする．西洋の伝統では自然数からはじめるのであるが，高木貞治の『数の概念』にならい，東洋の伝統を引き継いで，整数を定義し，有理数にすすむ．

第二，

実数の公理までまとめる．整数の公理は人間がつかんでいる数の世界の構造を定式化するものであるが，実数の公理は理論の要請である．実数の公理を満たすモデルの存在を，有理数をもとに示す．

実数の構成でのカントールの方法はそれ数列を用いる．実数の連続性を理論の根拠として，そこから導かれる，数列の極限に関する基本性質と無限級数についてまとめる．

第三，

解析学は関数を解析することが，基本である．ではその関数とは何か．また，関数の連続性とは何か．これをいわゆる 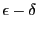$\epsilon -\delta$論法によって定義し，基本性質を示す．

第四，

無限小変化率として微分をとらえ，関数の微分を定義し，基本定理としての平均値の定理を示す．平均値の定理の一般化として，関数の展開定理を示す．

第五，

無限小の総和としての積分を微分とは独立に定義する．そのうえで面積，体積などの量と定積分の関係を考える．また，積分と微分がどのような条件で逆演算であるかを解明する．

第六，

微分と積分を多次元空間の関数に適用し，陰関数定理を証明する．ベクトル解析と多変数の微分積分の初歩をつかむ．

第七，

微分方程式を定義し，実数の完備性がどのように微分方程式の解の存在を保証するのかを確認する．

第八，

以上の準備の下に，物理世界への適用として，地球の軌道が太陽を焦点とする楕円軌道をなすことを証明する．

第九，

複素関数は微分において，実関数の微分とまったく異なる様相を見せる．複素関数の微分可能性は，実関数のそれよりはるかに厳しい条件である．これを確認したうえで，積分を定義し，コーシーの積分定理を証明し，それをもとに，正則関数の基礎づけをおこなう．

第十，

正則関数は，さらに解析関数としてとらえてはじめてその意味が明確になる．それがまた，多様体上の関数としてあたらな定義と発展の第一歩となる．このあたりまでを述べ，いくつか，実関数論への応用にふれて稿を終えたい．

高校などで数学教育に携わる人，解析学への道筋を知りたい大学初年級の学生，そして意欲的な高校生等にいささかの役に立てればと思う．

解析学はここから大きくさまざまの分野に展開する．一方で，ルベーグ測度論に深まり，また複素関数の解析，複素函数論にすすむ．そうしてはじめて実関数の解析もまたその意味が明らかになる．さらに，複素関数の解析からリーマン面へ，そして代数幾何と複素多様体に展開する．そのことをここで指摘し，さらなる勉強をすすめたい．

記述を簡明にするため，■で定義や定理，命題等の陳述の終わりを示し，□で証明の終わりを示すことにする．「系」とは定理からただちに導かれる命題，または定理の圏内にあって，関連する他の命題と結合することで示される命題を意味し，番号は「定理番号−系番号」となっている．