

 次: 対応と写像
上: 集合と公理
前: 集合と公理
次: 対応と写像
上: 集合と公理
前: 集合と公理
集合論は,古典的な解析学を根本的に変革し,現代数学に不可欠な数学の言葉となった.言葉が伝達の方法であると同時に思想の母体であるように,集合論は現代の数学記述の言葉であると同時に考え方の基礎である.この集合の考え方と記法を整理するところからはじめよう.
また,高校時代に学ぶべき数学の全体像を一言でいえば,集合と写像である.このような観点からも,集合についてあらかじめ一定のことを考えておかなければならない.
そもそも集合とは何か.現行の日本の高校数学課程では次のように書かれている.ある教科書の記述である.
1から10までの自然数の集まりのように,それに含まれる「もの」がはっきりしているような,「もの」の集まりを集合という.集合に含まれている1つ1つの「もの」を,その集合の要素という.
これによると「美しいものの集まり」が集合となり得ないのは,あるものがその集合に属するか否かが個人の主観によって異なり,確定できないからである.だからどのようなものを集めるのかが大切なのだ.ところで「はっきりしている」という意味ははっきりしてるだろうか.
この教科書の定義を次のようにとらえ直そう.ある枠組のなかで考えているものを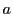 や
や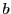 のように小文字で表し,それらを一つにまとめたものを
のように小文字で表し,それらを一つにまとめたものを のように大文字で表す.書体は何でもよい.
のように大文字で表す.書体は何でもよい. にまとめられた個々のものを集合
にまとめられた個々のものを集合 の要素という.元ともいうが,高校教科書にあわせて要素といおう.
の要素という.元ともいうが,高校教科書にあわせて要素といおう.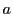 が
が の要素であることを
の要素であることを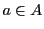 と書く.この記号を用いて,集合という概念の定義を明示的に書く.
と書く.この記号を用いて,集合という概念の定義を明示的に書く.
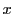 が
が に含まれることを
に含まれることを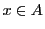 ,含まれないことを
,含まれないことを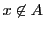 と書く.
また
と書く.
また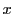 と
と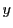 が相等しいことを
が相等しいことを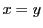 ,等しくないことを
,等しくないことを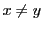 と書く.
と書く.
後にのべるように,この条件を満たすものとして, をそれ自身を要素に含まないような集合の集合とすると,
をそれ自身を要素に含まないような集合の集合とすると, が
が に含まれるとしても,含まれないとしても矛盾が起こる.この問題は「集合の公理」で考えることにし,今は素朴な集合のとらえ方を定式化した上記定義からはじめよう.
に含まれるとしても,含まれないとしても矛盾が起こる.この問題は「集合の公理」で考えることにし,今は素朴な集合のとらえ方を定式化した上記定義からはじめよう.
集合がいかなるものかはわかった.つまり集合という概念は定義された.それではこの集合そのものはどのように定義するのか.直接的には,要素を書き並べることでどのような集合であるかが確定する.記号では
のように書く.このようにして集合を定義することを外延的定義という.これはそのまますべてを書いただけである.逆にこの場合,集合が「15の約数の集合である」と見抜くことは大切なことである.もちろん外延的に定義された集合にこのような性質があるとはかぎらない.逆にいくつもあることもある.
外延的定義は無限集合には使えない.偶数をすべて書くことはできない.したがって要素をすべて書くのではない方法で集合を定義しなければならない.それは「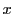 は〜である」という条件によって集合を定義することである.つまり,集合
は〜である」という条件によって集合を定義することである.つまり,集合 は「
は「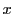 に関する条件
に関する条件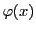 を満たす
を満たす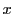 よりなるもの」として定めるのである.
よりなるもの」として定めるのである.
偶数の集合は,条件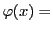 「
「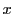 は偶数である」を満たす
は偶数である」を満たす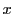 の全体を
の全体を とすることで定義するのである.このような集合の定義を内包的定義という.内包的に定義された集合
とすることで定義するのである.このような集合の定義を内包的定義という.内包的に定義された集合 は
は
のように書くことができる.実際には「満たす」がなくても意味が不明にならないときは条件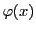 のみを記しておく.では
のみを記しておく.では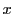 はどの範囲からとるのか.一定の全体集合を定めておいていくつかの集合をその全体集合からとって考えるというようにすることも多い.そのような集合を普遍集合ということもある.
はどの範囲からとるのか.一定の全体集合を定めておいていくつかの集合をその全体集合からとって考えるというようにすることも多い.そのような集合を普遍集合ということもある.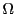 や
や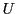 などを使うことが多い.一方,要素をもたない空の集合も考える.これを空集合といい
などを使うことが多い.一方,要素をもたない空の集合も考える.これを空集合といい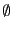 と書くことにする.
と書くことにする.
内包的定義は新しい局面を開く.集合というのは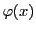 が真となるすべての要素からなることを意味し,具体的にそれがどのようなものであるかはわからなくても,そのすべてを考えるということになる.偶数の集合というとき,偶数の一つ一つをすべて確認するわけではない.しかし,数
が真となるすべての要素からなることを意味し,具体的にそれがどのようなものであるかはわからなくても,そのすべてを考えるということになる.偶数の集合というとき,偶数の一つ一つをすべて確認するわけではない.しかし,数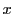 が偶数の集合に属するか属さないかは確定する.
が偶数の集合に属するか属さないかは確定する.
二つの集合 と
と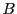 に対して,
に対して,
とする.集合 と
と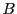 に対して積集合は
に対して積集合は の要素で
の要素で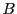 の要素でもあるものからなる部分集合であるが,和集合の存在は自明ではない.それに対する数学の外での議論は置いて,数学では,後に述べる集合の公理系に,和集合の存在公理を置き,それを出発とする.逆にいえば,新たな矛盾や問題点が出てくるまでは,和集合の存在は数学のなかでは議論しないのである.
の要素でもあるものからなる部分集合であるが,和集合の存在は自明ではない.それに対する数学の外での議論は置いて,数学では,後に述べる集合の公理系に,和集合の存在公理を置き,それを出発とする.逆にいえば,新たな矛盾や問題点が出てくるまでは,和集合の存在は数学のなかでは議論しないのである.
集合 に対し,その部分集合全体の集合を
に対し,その部分集合全体の集合を のべき集合といい,
のべき集合といい,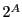 などと書き表す.ただし,集合
などと書き表す.ただし,集合 の部分集合には,空集合と集合
の部分集合には,空集合と集合 それ自身を含めるものとする.例えば
それ自身を含めるものとする.例えば
と3個の要素からできているとき,べき集合は
と8個の要素からなる.なぜ8個になるのか.集合 の要素は3個あり,各要素が選ばれるか選ばれないか,それぞれ2通りなので
の要素は3個あり,各要素が選ばれるか選ばれないか,それぞれ2通りなので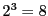 つの場合がる.それに応じて部分集合も8個あるのである.
つの場合がる.それに応じて部分集合も8個あるのである.
べき集合の8個の要素の一つを選ぶと,それに対して集合 から集合
から集合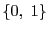 への写像
への写像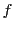 が定まる.つまり
が定まる.つまり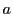 が選ばれた部分集合に含まれるか含まれないかに応じて,
が選ばれた部分集合に含まれるか含まれないかに応じて,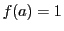 または
または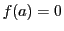 と定めるのである.逆に集合
と定めるのである.逆に集合 から集合
から集合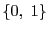 への写像
への写像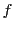 に対し
に対し
によって の部分集合が定まる.このように,
の部分集合が定まる.このように, の部分集合と集合
の部分集合と集合 から集合
から集合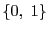 への写像
への写像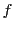 は一対一に対応している.
は一対一に対応している.
これを一般化し,二つの集合 と
と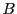 に対し,集合
に対し,集合 から集合
から集合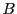 への写像の集合をべき集合といい
への写像の集合をべき集合といい
と書く.先に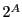 と書いたのは,この場合
と書いたのは,この場合
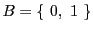 となり,
となり,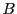 の要素の個数が2だからである.べき集合の存在もまた公理系に入れることで,その存在についての議論は,現在の数学では行わない.
の要素の個数が2だからである.べき集合の存在もまた公理系に入れることで,その存在についての議論は,現在の数学では行わない.
集合 ,
,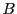 の直積
の直積 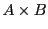 を次のように定義する.
を次のように定義する.
同じ集合 の直積は
の直積は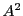 とも書く.先のべき集合の記号の用法からすれば,
とも書く.先のべき集合の記号の用法からすれば,
でもなければ記号の整合性がとれないのであるが,
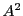 の要素
の要素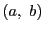 と
と
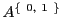 の
の
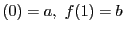 となる要素
となる要素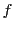 を対応させることにより,これは一対一対応になる.
を対応させることにより,これは一対一対応になる.
例 1.1
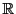
を実数の集合とする.
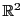
は2つの実数の順序づけられた組
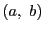
よりなる.
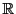
は数直線でもあるのだが,
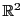
は平面の点と対応する.この対応を定めるためには,平面の1次独立な2つのベクトル
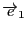
,
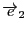
が必要である.
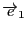
,
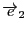
によって
に平面上の
ベクトル
で定まる点を対応させるのである.
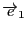
,
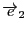
が大きさが1で直交しているとき,この平面を直交座標平面というのであった.大きさが1で直交しているという条件がみたされなくても,
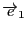
,
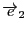
が1次独立であれば平面上の点を一意に定める.これを一般的には斜交座標という.『数学対話』「座標の方法」参照のこと.
直積集合の存在もまた公理系に入れることで,その存在についての議論は,現在の数学では行わない.
日本の高校でも「集合」の概念は習う.しかし,実際に扱うのは要素の個数が有限である場合がほとんどだった.実は,集合は無限集合を考えるとき,面白く不思議なことが起こる.自然数の集合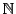 と正の偶数の集合
と正の偶数の集合 という二つの集合を考えよう.
という二つの集合を考えよう.
である.しかし
を対応させると,これは 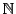 の要素と
の要素と  の要素の間の一対一の対応だ.つまり
の要素の間の一対一の対応だ.つまり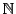 と
と の要素は「同じだけ」ある! 部分が全体と等しい? 無限集合ではこのように部分集合の各要素と全体集合の各要素の間に一対一の対応ができることがある.これがさらに実数の集合に至って驚くようなことが起こるのである.これは後に述べる.
の要素は「同じだけ」ある! 部分が全体と等しい? 無限集合ではこのように部分集合の各要素と全体集合の各要素の間に一対一の対応ができることがある.これがさらに実数の集合に至って驚くようなことが起こるのである.これは後に述べる.
集合に対してそれを操作して新しい集合を考えたり,集合相互の関係を考えたりすることが重要である.普遍集合を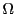 とする.集合の相互関係は論理と密接な関係を持っている.
とする.集合の相互関係は論理と密接な関係を持っている.
記号「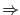 」は「ならば」を意味し,二つの命題
」は「ならば」を意味し,二つの命題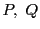 に対して「
に対して「
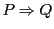 」は命題
」は命題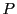 が成立するなら(真なら)命題
が成立するなら(真なら)命題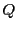 が成立する(真である)ことを意味する.また記号「
が成立する(真である)ことを意味する.また記号「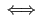 」は「必要十分である」「同値である」を意味し,二つの命題
」は「必要十分である」「同値である」を意味し,二つの命題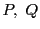 に対して「
に対して「 」は命題
」は命題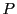 が成立することと命題
が成立することと命題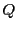 が成立することが同値であることを意味する.
が成立することが同値であることを意味する.
- まず集合の包含関係である.
が成り立つとき,集合 は集合
は集合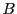 に含まれるといい,
次のように書く.
に含まれるといい,
次のように書く.
- 集合
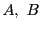 に対し,
その和集合
に対し,
その和集合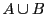 を次のように定める.
を次のように定める.
- 集合
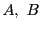 に対し,
その積集合
に対し,
その積集合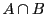 を次のように定める.
を次のように定める.
- 集合
 に対し,
その補集合
に対し,
その補集合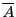 を次のように定める.
を次のように定める.
集合は一定の条件を満たすものすべての集合なのであるから,集合の間に成り立つ関係や集合から作られた集合には,条件の関係が対応する.それを次にまとめておこう.
二つの集合が二つの条件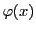 と
と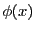 で定められているとする.
で定められているとする.
このとき,集合の関係は条件の関係に対応している.
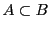 であることは
であることは
となり,
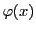 が
が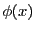 の
十分条件(または
の
十分条件(または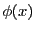 が
が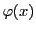 の必要条件)であることと
同じことを意味することがわかる.
の必要条件)であることと
同じことを意味することがわかる.
- 二つの条件
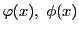 に対して,
条件「
に対して,
条件「
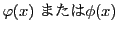 」を
」を
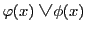 と書き,
条件「
と書き,
条件「
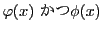 を
を
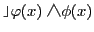 と書く.
と書く.
集合の和と積に対しては次のような条件が対応する.
-
- 補集合は条件
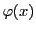 の否定に対応する.
の否定に対応する.
これは次のように示される.
だからド・モルガンの法則は次の条件の「かつ(∧)」「または(∨)」「否定(
 )」に関する法則が対応する.
)」に関する法則が対応する.
このように集合と論理は一体である.
今後,必要に応じて用いる論理記号をここで確認しておこう.「条件」とは何か.今はこれを,変数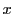 を含む命題とする.
を含む命題とする.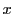 に
に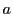 を代入したとき,それが真になることを「
を代入したとき,それが真になることを「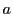 は条件
は条件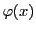 をみたす」という.
をみたす」という.
「集合 の任意の要素
の任意の要素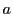 は条件
は条件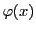 をみたす.」これを
をみたす.」これを
のように書く.記号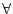 は「すべての」という意味である.この記号を全称記号という.
は「すべての」という意味である.この記号を全称記号という.
「条件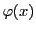 をみたす集合
をみたす集合 の要素
の要素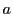 が存在する.」これを
が存在する.」これを
のように書く.記号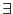 は「存在する」という意味である.この記号を存在記号という.
は「存在する」という意味である.この記号を存在記号という.
これらの記号で指定される演算や操作は,ある集合の要素の範囲を限定することになるので,量化子や限定記号といわれる.
もとより論理にどのような操作まで許すのかという,論理の公理についても考えなければならないのだが,本稿では,高校での数学で教科書にある範囲は,そこに考えるべき問題があることを指摘し,その考察は保留しつつ,そのまま用いる.


 次: 対応と写像
上: 集合と公理
前: 集合と公理
次: 対応と写像
上: 集合と公理
前: 集合と公理
2014-05-23
![]() や
や![]() のように小文字で表し,それらを一つにまとめたものを
のように小文字で表し,それらを一つにまとめたものを![]() のように大文字で表す.書体は何でもよい.
のように大文字で表す.書体は何でもよい.![]() にまとめられた個々のものを集合
にまとめられた個々のものを集合![]() の要素という.元ともいうが,高校教科書にあわせて要素といおう.
の要素という.元ともいうが,高校教科書にあわせて要素といおう.![]() が
が![]() の要素であることを
の要素であることを![]() と書く.この記号を用いて,集合という概念の定義を明示的に書く.
と書く.この記号を用いて,集合という概念の定義を明示的に書く.
![]() が
が![]() に含まれることを
に含まれることを![]() ,含まれないことを
,含まれないことを![]() と書く.
また
と書く.
また![]() と
と![]() が相等しいことを
が相等しいことを![]() ,等しくないことを
,等しくないことを![]() と書く.
と書く.
![]() をそれ自身を要素に含まないような集合の集合とすると,
をそれ自身を要素に含まないような集合の集合とすると,![]() が
が![]() に含まれるとしても,含まれないとしても矛盾が起こる.この問題は「集合の公理」で考えることにし,今は素朴な集合のとらえ方を定式化した上記定義からはじめよう.
に含まれるとしても,含まれないとしても矛盾が起こる.この問題は「集合の公理」で考えることにし,今は素朴な集合のとらえ方を定式化した上記定義からはじめよう.
![]() は〜である」という条件によって集合を定義することである.つまり,集合
は〜である」という条件によって集合を定義することである.つまり,集合![]() は「
は「![]() に関する条件
に関する条件![]() を満たす
を満たす![]() よりなるもの」として定めるのである.
よりなるもの」として定めるのである.
![]() 「
「![]() は偶数である」を満たす
は偶数である」を満たす![]() の全体を
の全体を![]() とすることで定義するのである.このような集合の定義を内包的定義という.内包的に定義された集合
とすることで定義するのである.このような集合の定義を内包的定義という.内包的に定義された集合![]() は
は
![]() が真となるすべての要素からなることを意味し,具体的にそれがどのようなものであるかはわからなくても,そのすべてを考えるということになる.偶数の集合というとき,偶数の一つ一つをすべて確認するわけではない.しかし,数
が真となるすべての要素からなることを意味し,具体的にそれがどのようなものであるかはわからなくても,そのすべてを考えるということになる.偶数の集合というとき,偶数の一つ一つをすべて確認するわけではない.しかし,数![]() が偶数の集合に属するか属さないかは確定する.
が偶数の集合に属するか属さないかは確定する.

![]() から集合
から集合![]() への写像
への写像![]() が定まる.つまり
が定まる.つまり![]() が選ばれた部分集合に含まれるか含まれないかに応じて,
が選ばれた部分集合に含まれるか含まれないかに応じて,![]() または
または![]() と定めるのである.逆に集合
と定めるのである.逆に集合![]() から集合
から集合![]() への写像
への写像![]() に対し
に対し
![]() と
と![]() に対し,集合
に対し,集合![]() から集合
から集合![]() への写像の集合をべき集合といい
への写像の集合をべき集合といい
![]() の直積は
の直積は![]() とも書く.先のべき集合の記号の用法からすれば,
とも書く.先のべき集合の記号の用法からすれば,
![]() 」は「ならば」を意味し,二つの命題
」は「ならば」を意味し,二つの命題![]() に対して「
に対して「
![]() 」は命題
」は命題![]() が成立するなら(真なら)命題
が成立するなら(真なら)命題![]() が成立する(真である)ことを意味する.また記号「
が成立する(真である)ことを意味する.また記号「![]() 」は「必要十分である」「同値である」を意味し,二つの命題
」は「必要十分である」「同値である」を意味し,二つの命題![]() に対して「
に対して「![]() 」は命題
」は命題![]() が成立することと命題
が成立することと命題![]() が成立することが同値であることを意味する.
が成立することが同値であることを意味する.
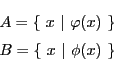
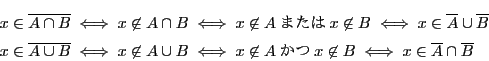
![]() )」に関する法則が対応する.
)」に関する法則が対応する.
![]() の任意の要素
の任意の要素![]() は条件
は条件![]() をみたす.」これを
をみたす.」これを
![]() をみたす集合
をみたす集合![]() の要素
の要素![]() が存在する.」これを
が存在する.」これを