などと書きあらわす.
集合![]() を定義域という.写像
を定義域という.写像
![]() によって
によって![]() の要素
の要素![]() に対応する
に対応する![]() の要素を
の要素を![]() と書き,これを
と書き,これを![]() による
による![]() の像,または
の像,または![]() の
の![]() における値という.また値の集合
における値という.また値の集合
![]() を写像
を写像![]() の値域という.
の値域という.
![]() と略記することもある.
■
と略記することもある.
■
集合![]() を定義域という.写像
を定義域という.写像
![]() によって
によって![]() の要素
の要素![]() に対応する
に対応する![]() の要素を
の要素を![]() と書き,これを
と書き,これを![]() による
による![]() の像,または
の像,または![]() の
の![]() における値という.また値の集合
における値という.また値の集合
![]() を写像
を写像![]() の値域という.
の値域という.
![]() と略記することもある.
■
と略記することもある.
■
同値関係があると,同値なものをひとつの部分集合にまとめることができる.つまり![]() の要素
の要素![]() と同値な要素からなる
と同値な要素からなる![]() の部分集合
の部分集合![]() が一意に確定し,
が一意に確定し,
![]() のすべての要素はいずれかただひとつの
のすべての要素はいずれかただひとつの![]() に属する.いいかえると,任意の
に属する.いいかえると,任意の![]() と
と![]() について
について
![]() か
か
![]() のいずれか一方が成立する.
のいずれか一方が成立する.
![]() の属する集合を
の属する集合を![]() の同値類という.このようにして得られる同値類の集合
の同値類という.このようにして得られる同値類の集合
![]() から〜による商集合
から〜による商集合![]() への写像
への写像![]() を
を![]() に対して
に対して
![]() がふたたび加法と乗法をもつことも確認することができる.
がふたたび加法と乗法をもつことも確認することができる.
同値関係であるから,集合の集合のこの同値関係によるによる類別を考え,その類を集合![]() の濃度といい,
の濃度といい,![]() と記す,と考えてよいのか.集合の集合という考えかたには矛盾が生じるので,この定義を用いることはできない.
と記す,と考えてよいのか.集合の集合という考えかたには矛盾が生じるので,この定義を用いることはできない.
有限集合の場合は,その個数が等しければ一対一対応が存在し,逆も成り立つので,集合![]() の要素の個数を濃度とし,
の要素の個数を濃度とし,![]() と記す.実はここにも問題はある.つまり未だわれわれは「個数」を定義していないのである.このように,厳密に考えると,様々の問題を浮かびあがらせることが出来ることを忘れず,しかし,素朴な理解を重視して,考えてゆきたい.
と記す.実はここにも問題はある.つまり未だわれわれは「個数」を定義していないのである.このように,厳密に考えると,様々の問題を浮かびあがらせることが出来ることを忘れず,しかし,素朴な理解を重視して,考えてゆきたい.
集合![]() が集合
が集合![]() のなかに埋め込める,つまり
のなかに埋め込める,つまり![]() の部分集合との間に一対一対応が存在するとき,濃度の関係は
の部分集合との間に一対一対応が存在するとき,濃度の関係は![]() であると書く.
であると書く.![]() ではあるが,
ではあるが,![]() と
と![]() の間の一対一対応は存在しないときは
の間の一対一対応は存在しないときは![]() と書く.
と書く.
一般に,
証明
![]() の要素
の要素![]() に対して,
に対して,![]() から集合
から集合![]() への写像
への写像![]() を
を
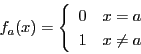
集合![]() と
と![]() の間に一対一対応が存在すると仮定する.
の間に一対一対応が存在すると仮定する.
この一対一対応で集合![]() の要素
の要素![]() に対応する
に対応する![]() の部分集合を
の部分集合を![]() とする.
とする.
![]() の部分集合
の部分集合![]() を次のように定める.
を次のように定める.
いずれも矛盾となる.ゆえに集合![]() と
と![]() の間に一対一対応は存在しない.つまり
の間に一対一対応は存在しない.つまり
上記背理法はいわゆる対角線論法である.
自然数とと一対一の対応が作れる無限集合の濃度を
可付番と言い,![]() と書き表し「アレフ0」と読む.また可付番な無限を可算無限ともいう.
と書き表し「アレフ0」と読む.また可付番な無限を可算無限ともいう.
それに対して実数の集合の濃度を![]() と書く.
カントールが最初に発見した集合論の定理が,次の定理である.
この定理は,実数の集合の濃度は自然数の濃度より大きい,
つまり実数の集合は可付番ではないことを意味する.
カントールは1874年にはこれを発見していたが,
1891年に次の証明のような対角線論法でこれを証明した.
カントールは三角関数の級数の研究から集合論を創始し,また,
位相空間論の基礎を築いた.現代的な数学のはじまりとなったものだ.
と書く.
カントールが最初に発見した集合論の定理が,次の定理である.
この定理は,実数の集合の濃度は自然数の濃度より大きい,
つまり実数の集合は可付番ではないことを意味する.
カントールは1874年にはこれを発見していたが,
1891年に次の証明のような対角線論法でこれを証明した.
カントールは三角関数の級数の研究から集合論を創始し,また,
位相空間論の基礎を築いた.現代的な数学のはじまりとなったものだ.
これは,区間![]() の実数
の実数![]() を2進法で
を2進法で
よって上記定理から,区間![]() の濃度は自然数よりも実際に大きいことがわかる.
つまり
の濃度は自然数よりも実際に大きいことがわかる.
つまり
無限集合に対して,
となる集合という命題がいわゆる一般連続体仮説である.次節で述べるようにこれは公理的集合論のなかで証明することも否定することもできない.集合論の公理系から独立している.は存在しない.