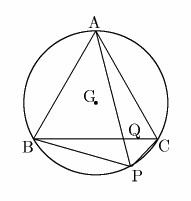
△ABQ ∽ △CPQ である.これから AQ・QP=BQ・QC (ほうべきの定理) .
一方 △ABC が正三角形であるから,円周角の相等とあわせて
京大文理共通第1問解説 問題 2000年入試に戻る
正三角形である ⇔ 重心と外心が一致する |
この単純なことがしっかりおさえられていないと計算が複雑になります.
最近の京大の文理共通問題は易しかったので,そのつもりで,まずこれを片づけてと思ったら,意外に計算しきれず焦った人が多かったようです.
上の単純なこと,この機会に自分で確認しておきましょう.
なおこの問題は純粋に図形の問題としてもできます.

△ABQ ∽ △CPQ である.これから AQ・QP=BQ・QC (ほうべきの定理) .
一方 △ABC が正三角形であるから,円周角の相等とあわせて
∠ABQ=∠APB.よって,△ABQ ∽ △APB .よって
AQ:AB=AB:AP
そこでAB=a ,AQ=x ,QP=y とおく.
(1-p)pa2=xy , a2=x(x+y)
これから x2=a2(p2-p+1) となる.よって
k=(x+y)/x=a2/a2(p2-p+1)= 1/(p2-p+1)
となる.
京大の問題は,ベクトル,座標幾何 と見かけはいろいろでも,実際はほうべきの定理でできるものがたくさんあります.