千葉大7解説 問題 2000年入試に戻る
1.フェルマーの最終定理が解決して以降,この型の問題がよく出題される.その典型が次の1998年信州大学の問題である.
|
「n を2より大きい自然数とするとき 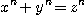 を満たす整数解 x, y, z (xyz ≠ 0) は存在しない.」というのは{フェルマーの最終定理として有名である.しかし多くの数学者の努力にもかかわらず一般に証明されていなかった.ところが1995年この定理がワイルスの100ページを越える大論文と,テイラーとの共著論文により与えられた.当然 を満たす整数解 x, y, z (xyz ≠ 0) は存在しない.」というのは{フェルマーの最終定理として有名である.しかし多くの数学者の努力にもかかわらず一般に証明されていなかった.ところが1995年この定理がワイルスの100ページを越える大論文と,テイラーとの共著論文により与えられた.当然
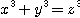 を満たす整数解 x, y, z (xyz ≠ 0) は存在しない. を満たす整数解 x, y, z (xyz ≠ 0) は存在しない.
さて,ここではフェルマーの定理を知らないものとして,次を証明せよ.
x, y, z を0でない整数とし,もしも等式 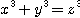 が成立しているならば, x, y, z のうち少なくとも1つは3の倍数である. が成立しているならば, x, y, z のうち少なくとも1つは3の倍数である.
|
この問題は背理法で証明しよう.すべてが3の倍数でないと仮定し,x=3l±1
,y=3m± 1,z=3n± 1 とおいて代入する.その両辺の9で割った余りを比べれば結論が出る.それから,このことを活用して,
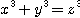 に整数解が存在しないことも証明してみよう.
に整数解が存在しないことも証明してみよう.
さて, (x, y, z)=(3, 4, 5), (5, 12, 13), (15, 8, 17), (7, 24, 25) などのように 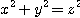 を満たす整数解 x, y, z (xyz ≠ 0) はピタゴラス数といわれる.ピタゴラス数は無数にある.ところが,n
≧3 となると
を満たす整数解 x, y, z (xyz ≠ 0) はピタゴラス数といわれる.ピタゴラス数は無数にある.ところが,n
≧3 となると 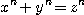 に解はない.フェルマ(Pierre de Fermat,1601〜1665)は,n ≧3 のとき解がないとのメモを本の余白に残しさらに「私はこの証明を発見したが,ここは狭くて書けない」とだけ書いたのです.以来300年,多くの人がこの証明を試み,それがまた数学を発展させたが,しかし肝心のフェルマーの定理自体はなかなか証明されなかった.私の学生時代は今世紀中にはとてもできないだろうと,みんな考えていた.ところが,数学のいろんな分野の発展を総合し,ついに1995年になって証明された.
に解はない.フェルマ(Pierre de Fermat,1601〜1665)は,n ≧3 のとき解がないとのメモを本の余白に残しさらに「私はこの証明を発見したが,ここは狭くて書けない」とだけ書いたのです.以来300年,多くの人がこの証明を試み,それがまた数学を発展させたが,しかし肝心のフェルマーの定理自体はなかなか証明されなかった.私の学生時代は今世紀中にはとてもできないだろうと,みんな考えていた.ところが,数学のいろんな分野の発展を総合し,ついに1995年になって証明された.
2.無限降下法
千葉大の問題は背理法で論述した.
すべてが0ではない解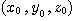 があれば,互いに素な解がある.これを改めて
があれば,互いに素な解がある.これを改めて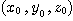 とする.ところがこのときすべてが2の倍数になる.互いに素という仮定と矛盾した.よって,すべてが0ではない解
とする.ところがこのときすべてが2の倍数になる.互いに素という仮定と矛盾した.よって,すべてが0ではない解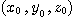 は存在しない.
は存在しない.
という論法であった.これは言い換えれば,
すべてが0ではない解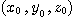 があれば,そのすべてが2の倍数になる.3数を2で割ったものを改めて
があれば,そのすべてが2の倍数になる.3数を2で割ったものを改めて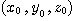 とする.これは同じ条件を満たすので,再びすべてが2の倍数である.これは無限にくりかえせる.つまり3数とも,素因数2を無数にもつ.これはあり得ない.
とする.これは同じ条件を満たすので,再びすべてが2の倍数である.これは無限にくりかえせる.つまり3数とも,素因数2を無数にもつ.これはあり得ない.
ということである.この論法を無限降下法という.この論法をはじめて方法として明確にしたのもフェルマである.近代の整数の研究は,すべてフェルマに始まる.無限降下法の一番簡単な例が教科書にも載っている,2の平方根が無理数であることの証明である.
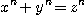 を満たす整数解 x, y, z (xyz ≠ 0) は存在しない.」というのは{フェルマーの最終定理として有名である.しかし多くの数学者の努力にもかかわらず一般に証明されていなかった.ところが1995年この定理がワイルスの100ページを越える大論文と,テイラーとの共著論文により与えられた.当然
を満たす整数解 x, y, z (xyz ≠ 0) は存在しない.」というのは{フェルマーの最終定理として有名である.しかし多くの数学者の努力にもかかわらず一般に証明されていなかった.ところが1995年この定理がワイルスの100ページを越える大論文と,テイラーとの共著論文により与えられた.当然
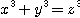 を満たす整数解 x, y, z (xyz ≠ 0) は存在しない.
を満たす整数解 x, y, z (xyz ≠ 0) は存在しない.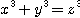 が成立しているならば, x, y, z のうち少なくとも1つは3の倍数である.
が成立しているならば, x, y, z のうち少なくとも1つは3の倍数である.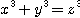 に整数解が存在しないことも証明してみよう.
に整数解が存在しないことも証明してみよう.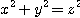 を満たす整数解 x, y, z (xyz ≠ 0) はピタゴラス数といわれる.ピタゴラス数は無数にある.ところが,n
≧3 となると
を満たす整数解 x, y, z (xyz ≠ 0) はピタゴラス数といわれる.ピタゴラス数は無数にある.ところが,n
≧3 となると 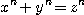 に解はない.フェルマ(Pierre de Fermat,1601〜1665)は,n ≧3 のとき解がないとのメモを本の余白に残しさらに「私はこの証明を発見したが,ここは狭くて書けない」とだけ書いたのです.以来300年,多くの人がこの証明を試み,それがまた数学を発展させたが,しかし肝心のフェルマーの定理自体はなかなか証明されなかった.私の学生時代は今世紀中にはとてもできないだろうと,みんな考えていた.ところが,数学のいろんな分野の発展を総合し,ついに1995年になって証明された.
に解はない.フェルマ(Pierre de Fermat,1601〜1665)は,n ≧3 のとき解がないとのメモを本の余白に残しさらに「私はこの証明を発見したが,ここは狭くて書けない」とだけ書いたのです.以来300年,多くの人がこの証明を試み,それがまた数学を発展させたが,しかし肝心のフェルマーの定理自体はなかなか証明されなかった.私の学生時代は今世紀中にはとてもできないだろうと,みんな考えていた.ところが,数学のいろんな分野の発展を総合し,ついに1995年になって証明された.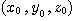 があれば,互いに素な解がある.これを改めて
があれば,互いに素な解がある.これを改めて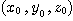 とする.ところがこのときすべてが2の倍数になる.互いに素という仮定と矛盾した.よって,すべてが0ではない解
とする.ところがこのときすべてが2の倍数になる.互いに素という仮定と矛盾した.よって,すべてが0ではない解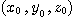 は存在しない.
は存在しない.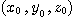 があれば,そのすべてが2の倍数になる.3数を2で割ったものを改めて
があれば,そのすべてが2の倍数になる.3数を2で割ったものを改めて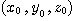 とする.これは同じ条件を満たすので,再びすべてが2の倍数である.これは無限にくりかえせる.つまり3数とも,素因数2を無数にもつ.これはあり得ない.
とする.これは同じ条件を満たすので,再びすべてが2の倍数である.これは無限にくりかえせる.つまり3数とも,素因数2を無数にもつ.これはあり得ない.