東大理系前期1 問題 解説 2001年入試に戻る
![]() の中点を
の中点を ![]() とする.
とする.
![]() はともに
1 辺 2 の正三角形なので
はともに
1 辺 2 の正三角形なので

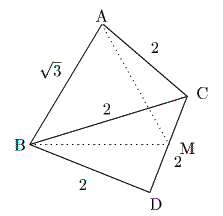
ゆえに,一般性を失うことなく次のように四面体を xyz 座標空間におくことが出来る.
![]() を xy 平面上におく.そのとき,点
を xy 平面上におく.そのとき,点 ![]() を x 軸の
負の部分におき,線分
を x 軸の
負の部分におき,線分 ![]() の中点が原点に来るようにする.
の中点が原点に来るようにする.
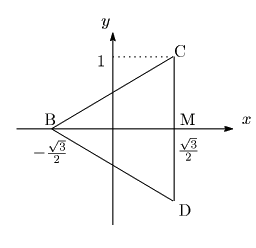
このとき
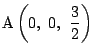 となり,他の
xy 平面上の各点の座標は図2のように
となり,他の
xy 平面上の各点の座標は図2のように
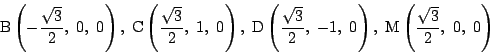
求める中心は対称性から xz 平面上にあり,さらに線分ABの垂直二等分線上にある.
この垂直二等分線は点Mを通り傾きが
![]() であるから
であるから
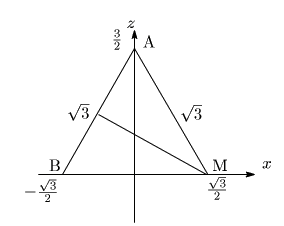
ゆえに求める中心 ![]() は
は
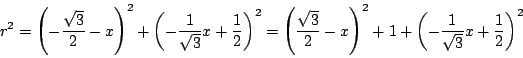
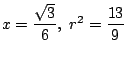 .
.