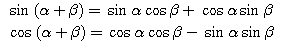n を自然数とする.次の等式が成り立つことを示せ.
(1)
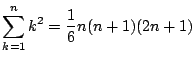 を証明せよ.
を証明せよ.
(2)
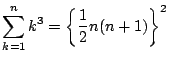 を証明せよ.
を証明せよ.
直線 ax+by+c=0 と点
を証明せよ.
原点を中心とする半径
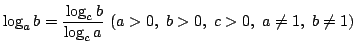 を証明せよ.
を証明せよ.
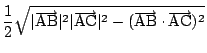 に等しいことを示せ.
に等しいことを示せ.
複素数
定数
が成り立つことを示せ.
区間
関数 f(x) は任意の実数 x に対して定義されているとする. f(x) が x=a において微分可能であることの定義を述べよ.
(1) 一般角
(2) (1)で述べた定義にもとづき,一般角
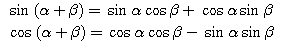
二つのベクトル
(1)
(2)
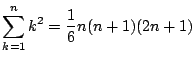 を証明せよ.
を証明せよ.
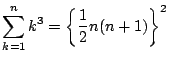 を証明せよ.
を証明せよ.
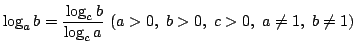 を証明せよ.
を証明せよ.
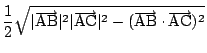 に等しいことを示せ.
に等しいことを示せ.