


次: 02千葉大
上: 背理法
前: 背理法
-
- (1)
- 結論の否定を仮定し,何らかの矛盾が生じることを示す.
それによって結論の否定が否定され,結論が成立することを示す
証明方法.
- (2)
-
![$\sqrt[3]{2}$](images/img35.gif) が有理数であると仮定する.
が有理数であると仮定する.
- 証明1
![$\sqrt[3]{2}=\dfrac{q}{p}\ (p\ と\ q\ は互いに素な整数)$](images/img67.gif) とおく.
とおく.
2p3=q3
となるので, q は偶数. q=2q' とおく.このとき
2p3=8q'3
より p も偶数となり,互いに素という仮定と矛盾した.
ゆえに
![$\sqrt[3]{2}$](images/img35.gif) は無理数.
は無理数.
- 証明2
![$\sqrt[3]{2}=\dfrac{q}{p}\ (p\ と\ q\ は整数)$](images/img68.gif) とおく.
とおく.
2p3=q3
となる.左辺の因数分解における因数2の個数は3で割ると1余る.
それに対して右辺の因数分解における因数2の個数は3の倍数.
素因数分解の一意性と矛盾した.
ゆえに
![$\sqrt[3]{2}$](images/img35.gif) は無理数.
は無理数.
- 証明3
![$\sqrt[3]{2}=\dfrac{q}{p}\ (p\ と\ q\ は0でない整数)$](images/img69.gif) とおく.
とおく.
2p3=q3
となるので, q は偶数. q=2q' とおく.このとき
2p3=8q'3
より p も偶数. p=2p' とおく.これを代入して約すると
2p'3=q'3
再び 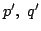 が2で約せ,これは何回でも繰り返せる.
つまり
が2で約せ,これは何回でも繰り返せる.
つまり 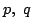 とも2で無限回約せる.
これは
とも2で無限回約せる.
これは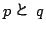 は0でない整数という仮定と矛盾した.
ゆえに
は0でない整数という仮定と矛盾した.
ゆえに
![$\sqrt[3]{2}$](images/img35.gif) は無理数.
は無理数.
AozoraGakuen
2002-09-04
![$\sqrt[3]{2}=\dfrac{q}{p}\ (p\ と\ q\ は互いに素な整数)$](images/img67.gif) とおく.
とおく.
![$\sqrt[3]{2}=\dfrac{q}{p}\ (p\ と\ q\ は互いに素な整数)$](images/img67.gif) とおく.
とおく.
![$\sqrt[3]{2}=\dfrac{q}{p}\ (p\ と\ q\ は整数)$](images/img68.gif) とおく.
とおく.
![$\sqrt[3]{2}=\dfrac{q}{p}\ (p\ と\ q\ は0でない整数)$](images/img69.gif) とおく.
とおく.