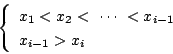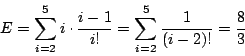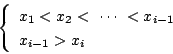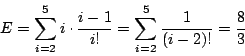上: 2. 解答
前: 4.
上: 2. 解答
前: 4.
-
- (1)
全事象の総数は
NPk である.それに対して
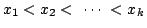 となる事象の各々は,
異なる k 個の数の組
となる事象の各々は,
異なる k 個の数の組
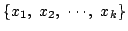 の各々と一対一に対応している.
すなわち,
NCk 通りある.
の各々と一対一に対応している.
すなわち,
NCk 通りある.
- (2)
同様に
となる事象の総数を求める.
異なる i 枚のカード
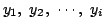 を選びその最大のものをxi-1に,
それ以外のi-1枚中の1枚を xi とし,他は小さい順に
を選びその最大のものをxi-1に,
それ以外のi-1枚中の1枚を xi とし,他は小さい順に
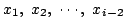 とすればよい.
残る k-i 枚は N-i から順に選んで並べればよい.ゆえに該当する事象の総数は
とすればよい.
残る k-i 枚は N-i から順に選んで並べればよい.ゆえに該当する事象の総数は
- (3)
求める得点の期待値を E とする.
AozoraGakuen
2002-03-04