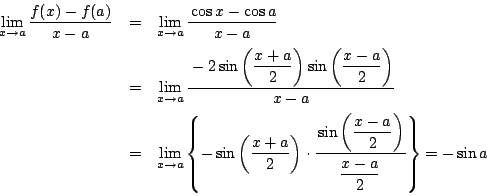次: 5.
上: 2. 解答
前: 3.
次: 5.
上: 2. 解答
前: 3.
-
- (1)
f(x) が x=a において微分可能であるとは
が存在することである.
- (2)
ii が正しい.なぜなら
f(x)=|x-a| は
となり x=a で連続である.しかし
より
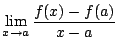 が存在しないので
微分可能ではない.
が存在しないので
微分可能ではない.
- (3)
関数
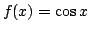 が x=a において連続であること,および
が x=a において連続であること,および
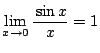 を用いて示す.
を用いて示す.
ゆえに, 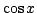 は確かに x=a で微分可能である.
は確かに x=a で微分可能である.
AozoraGakuen
2002-03-04
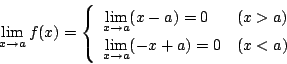
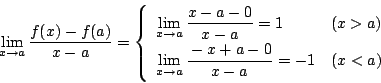
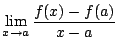 が存在しないので
微分可能ではない.
が存在しないので
微分可能ではない.
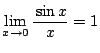 を用いて示す.
を用いて示す.
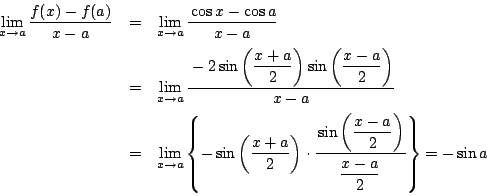
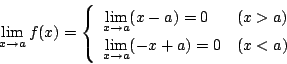
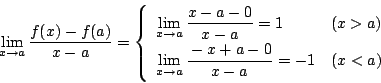
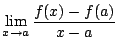 が存在しないので
微分可能ではない.
が存在しないので
微分可能ではない.
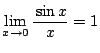 を用いて示す.
を用いて示す.