

 次: 2.
上: 1. 問題
前: 1. 問題
次: 2.
上: 1. 問題
前: 1. 問題
0でない複素数 z に対して, w=u+ivを
とするとき,次の問に答えよ。ただし,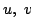 は実数, i は虚数単位で
ある。
は実数, i は虚数単位で
ある。
-
- (1)
複素数平面上で, z が単位円 |z|=1上を動くとき, w はどのような
曲線を描くか.
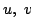 がみたす曲線の方程式を求め,その曲線を図示せよ.
がみたす曲線の方程式を求め,その曲線を図示せよ.
- (2)
複素数平面上で, z が実軸からの偏角
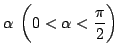 の半直線上を動くとき, w は
どのような曲線を描くか.
の半直線上を動くとき, w は
どのような曲線を描くか.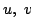 がみたす曲線の方程式を求め,その曲線を図示せよ.
がみたす曲線の方程式を求め,その曲線を図示せよ.
AozoraGakuen
2002-03-04
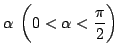 の半直線上を動くとき, w は
どのような曲線を描くか.
の半直線上を動くとき, w は
どのような曲線を描くか.