

 次: 6.
上: 2. 解答
前: 4.
次: 6.
上: 2. 解答
前: 4.
f(x)=x3+3ax2+3bx とおく.y=f(x) と y=c のグラフが相異なる
3つの交点を持つためには,関数 f(x) が極大値と極小値を持つことが必要である.
f'(x)=3x2+6ax+3bであるから
が相異なる実数解を持たねばならない.
が成立する.
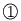 の2つの実数解を
の2つの実数解を
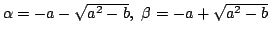 とする.このとき
f(x) は
とする.このとき
f(x) は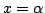 で極大,
で極大, 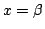 で極小である.
で極小である.
ここで
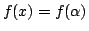 となる
となる 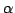 以外の xの値を
以外の xの値を 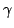 ,
,
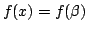 となる
となる 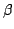 以外の xの値を
以外の xの値を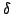 とする.
増減と値は次のようになる.
とする.
増減と値は次のようになる.
ゆえに2つのグラフが3つの交点を持つのは
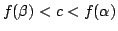 のときである.
のときである.
またこのとき y=f(x) と y=c の交点の x 座標は3つの開区間
に各々1つずつある.
の解が
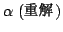 と
と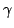 となるので
解と係数の関係から
となるので
解と係数の関係から
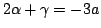 ゆえに
ゆえに
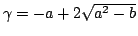 となる.
同様に
となる.
同様に
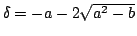 となる.
となる.
よって題意が示された.
AozoraGakuen
2002-03-01
![]() の2つの実数解を
の2つの実数解を
![]() とする.このとき
f(x) は
とする.このとき
f(x) は![]() で極大,
で極大, ![]() で極小である.
で極小である.![]() となる
となる ![]() 以外の xの値を
以外の xの値を ![]() ,
,
![]() となる
となる ![]() 以外の xの値を
以外の xの値を![]() とする.
増減と値は次のようになる.
とする.
増減と値は次のようになる.
