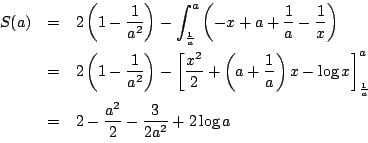これから
つまり
すなわち
第1式と第2式から ab=c(c-a+b),つまり (c-a)(c+b)=0 .
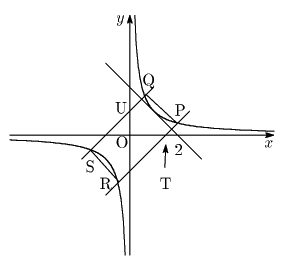 ゆえに直線
PRの式は
ゆえに直線
PRの式は
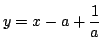 .この式で
y=0 として 点
T の x 座標を求める.
.この式で
y=0 として 点
T の x 座標を求める.
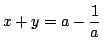 である.
対称性から,線分
TU が移動して最初に C と接する接点は
である.
対称性から,線分
TU が移動して最初に C と接する接点は 1<aの下でこれを解くと
であるから
つぎに線分 PQの式は
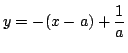 である.
である.
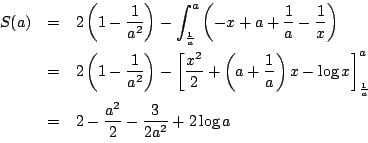
 ゆえに直線
PRの式は
ゆえに直線
PRの式は
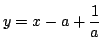 .この式で
y=0 として 点
T の x 座標を求める.
.この式で
y=0 として 点
T の x 座標を求める.
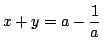 である.
対称性から,線分
TU が移動して最初に C と接する接点は
である.
対称性から,線分
TU が移動して最初に C と接する接点は 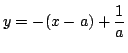 である.
である.