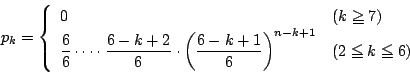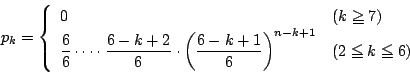次: 5.
上: 2. 解答
前: 3.
次: 5.
上: 2. 解答
前: 3.
-
- (1)
最初は任意で,以後直前に出た目と異なる目が出続ける事象である.
- (2)
さいころの目は6までなので
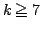 のときpk=0
のときpk=0
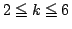 のとき.(1)と同様に考え,手前直近のk-1個の範囲内にある目とは
異なる目が出続ける事象である.手前直近のk-1個の範囲内にある目の個数
は1回目から k 回目の試行では
のとき.(1)と同様に考え,手前直近のk-1個の範囲内にある目とは
異なる目が出続ける事象である.手前直近のk-1個の範囲内にある目の個数
は1回目から k 回目の試行では
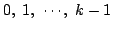 個で,
その後はつねに k-1個である.それら以外の目が出ればよい.
個で,
その後はつねに k-1個である.それら以外の目が出ればよい.
まとめて
- (3)
- 「 n 回の試行において,同じ目が続くことはなく,しかも同じ目が出る試行
の組でちょうど2だけ離れたものが少なくとも1組存在する」という事象は,いいかえれば
「 n 回の試行のうち,同じ目が出るどの2つの試行も 2 以上離れている」事象のうちで
「 n 回の試行のうち,同じ目が出るどの2つの試行も 3 以上離れている」ことがない
事象である.
ゆえにその確率は
AozoraGakuen
2002-03-01