
 上: 2. 解答
前: 4.
上: 2. 解答
前: 4.
-
- (1)
直線
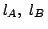 の方程式は
の方程式は
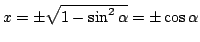 である.
円 C1 の方程式を y について解くと
である.
円 C1 の方程式を y について解くと
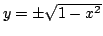 であり.
円 C2 の方程式を y について解くと
であり.
円 C2 の方程式を y について解くと
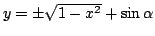 である.
2つの領域
である.
2つの領域 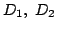 はそれぞれ
はそれぞれ
\[
\begin{array}{l}
D_1:\sqrt{1-x^2}\leqq y \leqq\sqrt{1-x^2}+\sin\alpha\\
D_2:-\sqrt{1-x^2}\leqq y \leqq-\sqrt{1-x^2}+\sin\alpha
\end{array}
\]
と表される.
したがって
- ここで
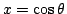 の置換を行うと,
の置換を行うと,
- この結果を代入して整理する.
\[
V_1(\alpha)=2\pi\left(\dfrac{\pi}{2}-\alpha \right)\sin\alpha+4\pi\sin^2\alpha\cos\alpha
\]
また
- (2)
- したがって
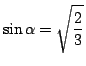 となる
となる 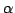 で極大かつ最大になる.
このとき
で極大かつ最大になる.
このとき
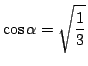 なので,最大値は
なので,最大値は
-
AozoraGakuen
2002-03-01
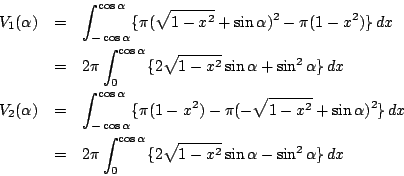
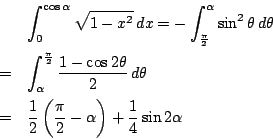
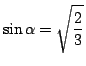 となる
となる 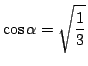 なので,最大値は
なので,最大値は