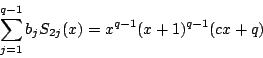次へ: 3番解答
上へ: 2006年入試問題研究
次へ: 3番解答
上へ: 2006年入試問題研究
数列の和の公式
などについて,次のような一般的な考察をしてみよう.
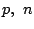 を自然数とする.
を自然数とする.
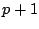 次の多項式
次の多項式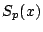 があって,
数列の和
があって,
数列の和
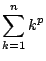 が
が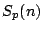 と表されることを示せ.
と表されることを示せ.
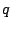 を自然数とする.(1)の多項式
を自然数とする.(1)の多項式
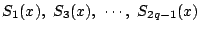 に対して,
に対して,
が恒等式となるような定数
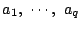 を
を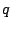 を用いて表せ.
を用いて表せ.
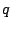 を2以上の自然数とする.
(1)の多項式
を2以上の自然数とする.
(1)の多項式
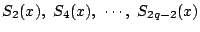 に対して,
に対して,
が恒等式となるような定数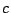 と
と
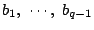 を
を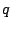 を用いて表せ.
を用いて表せ.
 を3以上の奇数とする.このとき,
を3以上の奇数とする.このとき,
を示せ.
参考 整数値をとる多項式・2000年東大後期
Aozora Gakuen
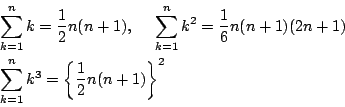
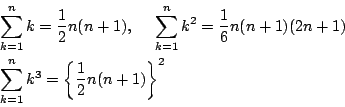
![]() を自然数とする.
を自然数とする.