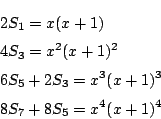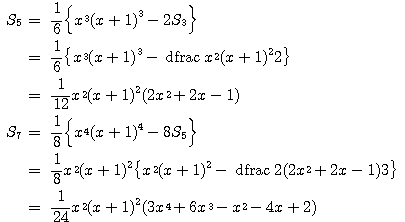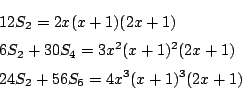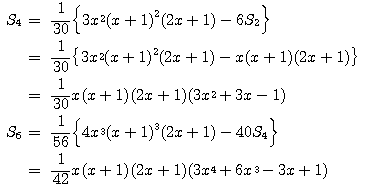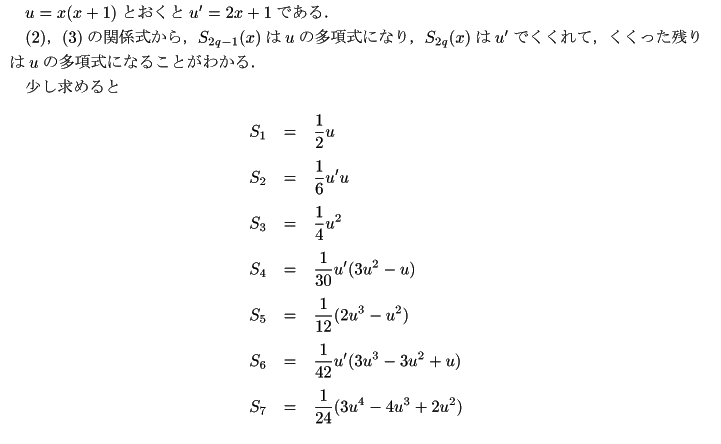![]() のとき.
のとき.
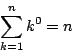
より
題意を満たす
![]() が存在したとする.
が存在したとする.
ここで二項定理から
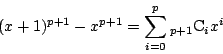
より
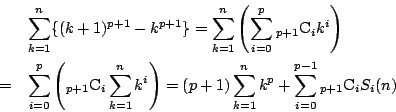
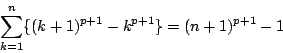
なので,
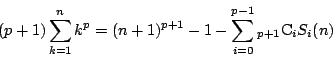
これから
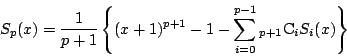
とおけばよい.
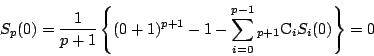
も成り立ち,
よって,0以上のすべての![]() に対して題意を満たす
に対して題意を満たす![]() が存在することが示された.
が存在することが示された.
したがって
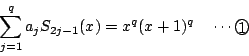
が恒等式となることと,
(1)から![]() は
は![]() のときには成立している.
のときには成立している.
命題:
が,すべての
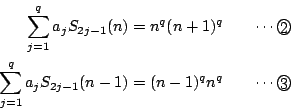
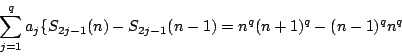
がすべての自然数で成立すればよい.ここで
である.よって
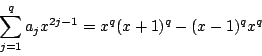
が,すべての
![\begin{eqnarray*}
&&x^q(x+1)^q-(x-1)^qx^q\\
&=&x^q\left\{\sum_{i=0}^q{}_q\mat...
...^{\left[\frac{q+1}{2}\right]}{}_q\mathrm{C}_{2l-1}x^{2q-(2l-1)}
\end{eqnarray*}](images/img46.png)
である.
これから,係数![]() を
を
のとき
となるようにとればよい.このとき
である. ただし,
この![]() に対しては0以上の任意の整数に対して
に対しては0以上の任意の整数に対して![]() が成立する.
が成立する.
つまりこのとき![]() は恒等式である.
は恒等式である.
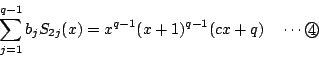
が恒等式となるためには,(2)と同様に考え,2以上の自然数
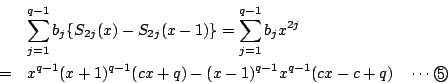
が恒等式となるように,定数
![\begin{eqnarray*}
&&x^{q-1}(x+1)^{q-1}(cx+q)-(x-1)^{q-1}x^{q-1}(cx-c+q)\\
&=&...
...=0}^{q-1}{}_{q-1}\mathrm{C}_{i}(-1)^ix^{q-1-i} \right\} \right]
\end{eqnarray*}](images/img56.gif)
ここで奇数次数の項をとると
で
となる.
が必要である.このとき偶数次の項は
で,
なので,このときこの項は
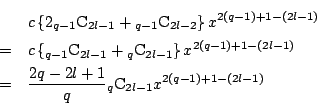
となる.
![]() が恒等式となるためには
が恒等式となるためには
ここで,
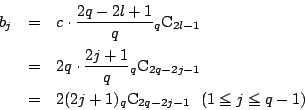
である. ただし
が成り立つことを
![]() のとき.
のとき.
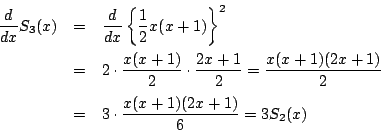
より成立する.
![]() が
が
![]() のとき成立するとする.
のとき成立するとする.
ここで![]() の両辺を
の両辺を![]() で微分する.
で微分する.
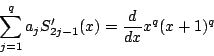
この等式において
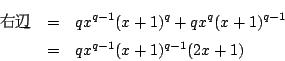
ところがこれは
よって![]() の左辺を
の左辺を![]() で微分した整式と
で微分した整式と![]() の左辺は等しい.
つまり
の左辺は等しい.
つまり
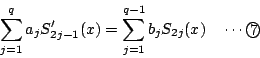
である.
ここで![]() の左辺で,
の左辺で,
![]() ,
,
![]() なので,
数学的帰納法の仮定を用いると
なので,
数学的帰納法の仮定を用いると
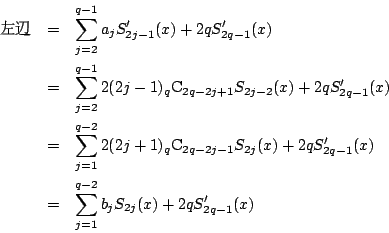
となる. これが
つまり
が示され,
したがって数学的帰納法によって,3以上の奇数![]() に対して
に対して![]() が成立する.
が成立する.