津田塾大解答
(1)
点 $ (a,\ f(a)) $ と点 $ (b,\ f(b)) $ を結ぶ線分の方程式は
\[
y=\dfrac{f(b)-f(a)}{b-a}(x-a)+f(a) (a< x< b)
\]
と表される.
ここで, $ F(x)=f(x)-\dfrac{f(b)-f(a)}{b-a}(x-a)-f(a) $ とおく.
平均値の定理から $ a< c< b $ で
\[
f'(c)=\dfrac{f(b)-f(a)}{b-a}
\]
となるものが存在する. $ F''(x)=f''(x)< 0 $ なので, $ F''(x) $ はこの区間で単調減少し,
$ F'(c)=f'(c)-\dfrac{f(b)-f(a)}{b-a}=0 $ であるから,
$ a< x< c $ で $ F'(x) >0 $ ,
$ c< x< b $ で $ F'(x)< 0 $ である.
さらに, $ F(a)=F(b)=0 $ なので,
\[
\left\{
\begin{array}{ll}
0=F(a)< F(x)\leqq F(c)&(a< x \leqq c)\\
F(c) >F(x)>F(b)=0&(c< x< b)
\end{array}
\right.
\]
となり,区間 $ (a,\ b) $ で $ F(x) >0 $ である.
したがって, $ y=f(x) $ のグラフは開区間 $ (a,\ b) $ において,
点 $ (a,\ f(a)) $ と点 $ (b,\ f(b)) $ を結ぶ線分の上側にある.
(2)
$ f(x)=\log x $ とする. $ f'(x)=\dfrac{1}{x} $ , $ f''(x)=-\dfrac{1}{x^2}< 0 $ である.
$ \dfrac{1}{p}+\dfrac{1}{q}=1 $ なので, $ x=\dfrac{1}{p}a+\dfrac{1}{q}b $ は,
区間 $ (a,\ b) $ の内分点である.
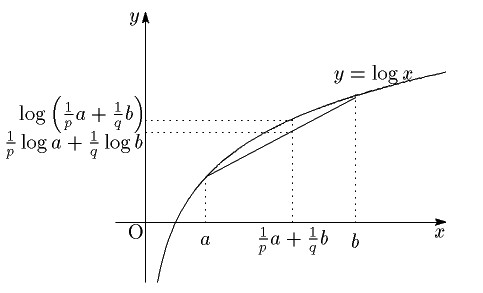
また,点 $ (a,\ f(a)) $ と点 $ (b,\ f(b)) $ を結ぶ線分と直線 $ x=\dfrac{1}{p}a+\dfrac{1}{q}b $ の交点の $ y $ 座標は,
$ y $ 軸における区間 $ (\log a,\ \log b) $ を同じ比で内分する点なので,
$ y=\dfrac{1}{p}\log a+\dfrac{1}{q}\log b $ である.
(3)
$ x=0 $ または $ y=0 $ なら $ x\geqq 0,\ y\geqq 0 $ より不等式
\[
xy\leqq \dfrac{x^p}{p}+\dfrac{y^q}{q}
\quad \cdots①
\]
は成立する.
$ x>0 $ かつ $ y>0 $ とする.
$ x^p=y^q $ なら $ k=x^p=y^q $ とおくと $ \dfrac{x^p}{p}+\dfrac{y^q}{q}=k $ であり,
$ xy=k^{\frac{1}{p}+\frac{1}{q}}=k $ なので,不等式 ① は等号で成立する.
$ x^p\ne y^q $ のとき, $ x^p< y^q $ とし, $ a=x^p,\ b=y^q $ で(2)を用いる.
\[
\dfrac{1}{p}\log x^p+\dfrac{1}{q}\log y^q\leqq \log\left(\dfrac{x^p}{p}+\dfrac{y^q}{q} \right)
\]
より
\[
\log xy\leqq \log\left(\dfrac{x^p}{p}+\dfrac{y^q}{q} \right)
\]
よって,この場合も不等式 ① は成立する.
$ x^p >y^q $ のときも同様である.
(4)
(3)より, $ i=1,\ 2,\ 3 $ に対して,
\[
|u_i||v_i| \leqq \dfrac{|u_i|^p}{p}+\dfrac{|v_i|^q}{q}
\]
がなりたつ. $ i=1,\ 2,\ 3 $ について辺々加えて
\[
\sum_{i=1}^3|u_i||v_i|\leqq \dfrac{1}{p}\sum_{i=1}^3|u_i|^p
+\dfrac{1}{q}\sum_{i=1}^3|v_i|^q
\]
一方,
\[
|u_1v_1+u_2v_2+u_3v_3|\leqq \sum_{i=1}^3|u_iv_i|=\sum_{i=1}^3|u_i||v_i|
\]
であり,
\[
\dfrac{1}{p}\sum_{i=1}^3|u_i|^p
+\dfrac{1}{q}\sum_{i=1}^3|v_i|^q=
\dfrac{1}{p}+\dfrac{1}{q}=1
\]
なので,
\[
|u_1v_1+u_2v_2+u_3v_3|\leqq 1
\]
が成り立つ.
本問の背景などは,
『数学対話』の中の「凸領域と不等式」を参照のこと.