東北大理系2番解答
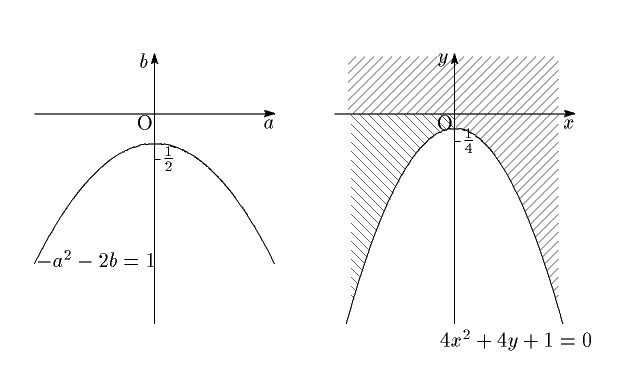
(1) 2つの放物線の方程式を連立して \[ (x-a)^2+b=-x^2 \] これから \[ 2x^2-2ax+a^2+b=0 \] が異なる2つの実数解をもち,その解の差が1となる. その判別式を $ D $ とすると, \[ D/4=a^2-2a^2-2b=-a^2-2b >0 \] このとき,2解を $ \alpha $ と $ \beta $ とすると,解と係数の関係と,条件 $ |\beta-\alpha|=1 $ から \[ (\beta-\alpha)^2=(\beta+\alpha)^2-4\alpha\beta=a^2-2(a^2+b)=-a^2-2b=1 \] この $ a $ と $ b $ は $ D >0 $ を満たす.頂点 $ (a,\ b) $ の軌跡は図左.
(2) $ C $ と $ D $ の2つの交点は $ (\alpha,\ -\alpha^2) $ , $ (\beta,\ -\beta^2) $ であるから, 2交点を結ぶ直線の方程式は \[ y=\dfrac{-\beta^2+\alpha^2}{\beta-\alpha}(x-\alpha)-\alpha^2=-(\alpha+\beta)x+\alpha\beta \] である.解と係数の関係を用いて,この係数を $ a $ と $ b $ で表すと, \[ y=-ax+\dfrac{a^2+b}{2} \] ここで, $ b=-\dfrac{a^2}{2}-\dfrac{1}{2} $ なので, \[ y=-ax+\dfrac{a^2}{4}-\dfrac{1}{4} \] である. $ a $ はすべての実数を動きうるので,点 $ (x,\ y) $ がこの直線の通過する領域の点である条件は, $ a $ の2次方程式を見たとき, $ a $ が実数となることと同値である. \[ a^2-4xa-4y-1=0 \] と変形されるので,その条件は判別式から \[ 4x^2+4y+1\geqq 0 \] である.この領域は図右.