京大特色3番解答
注意 $ y=x $ と $ y=\dfrac{1}{2c-x} $ の交点が \[ x=c\pm \sqrt{c^2-1} \] なので, $ 2c $ から $ \{x_n\} $ 数列を逆にたどり,いずれかをこの数列の初項にすることで, グラフの形状とあわせて,(1)と(2)は明らかである.
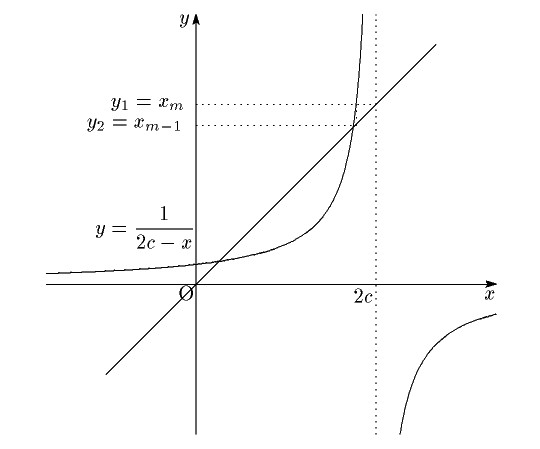
ただし論証は数列の論証として,行わねばならない.
(1)
条件(B)は,
\[
x_n=2c-\dfrac{1}{x_{n+1}}
\]
と書ける.そこで,数列 $ \{x_n\} $ を逆にたどる数列 $ \{y_n\} $ を
\[
y_1=2c,\ y_{n+1}=2c-\dfrac{1}{y_n}
\]
で定義する.
$ x_1=y_m $ とおけば, $ x_m=2c $ となるので, $ y_m $ は不都合な初項である.
無限に多くあることを示すために,数列 $ \{y_n\} $ は単調に減少し,
相異なる項の値が無限個であることを示せばよい.
$ n\geqq 2 $ のとき, $ 1< y_n< 2c $ であることを示す.
$ c>1 $ なので, $ y_2=2c-\dfrac{1}{2c} $ より,
$ 1< y_2< 2c $ である. $ 1< y_n< 2c $ とする.
$ \dfrac{1}{2c}< \dfrac{1}{y_n}< 1 $ のなで,
\[
2c-1< 2c-\dfrac{1}{y_n}< 2c-\dfrac{1}{2c}
\]
となり, $ 1< y_{n+1}< 2c $ である.よって $ n\geqq 2 $ のとき $ 1< y_n< 2c $ である.
$ y_1>y_2 $ である.
$ y_n>y_{n+1} $ とすれば,
$ -\dfrac{1}{y_n}>-\dfrac{1}{y_{n+1}} $ なので,
$ y_{n+1}>y_{n+2} $ となり,数学的帰納法から
$ y_n>y_{n+1} $ がつねに成立する.
よって(1)が示された.
(2)
(1)から $ y_n\leqq 2c $ なので,
いずれを初項にとっても $ q\leqq 2c $ は成立する.
$ c+\sqrt{c^2-1}< y_n $ を数学的帰納法で示す.
$ c+\sqrt{c^2-1}< c+c=y_1 $ である.
$ c+\sqrt{c^2-1}< y_n $ とする.
\begin{eqnarray*}
y_{n+1}&>&2c-\dfrac{1}{c+\sqrt{c^2-1}}=2c-\dfrac{1}{c+\sqrt{c^2-1}}\\
&=&2c-\left(c-\sqrt{c^2-1} \right)=c+\sqrt{c^2-1}
\end{eqnarray*}
より成立し,この結果(2)が示された.
(3)
$ c $ は $ 0< c< 1 $ にあるとする.このとき,数列 $ \{y_n\} $ の一般項を求める.
\[
t=2c-\dfrac{1}{t}
\]
を満たす $ t $ は $ t=c\pm \sqrt{c^2-1} $ で $ 0< c< 1 $ から $ t $ は虚数である.
これを $ \beta=c+\sqrt{c^2-1} $ , $ \alpha=c-\sqrt{c^2-1} $ とする.
$ \alpha\beta=1 $ なので, $ \cos\theta=c $ となる $ \theta $ がとれ,
$ \beta=\cos\theta+i\sin\theta $ ,
$ \alpha=\cos\theta-i\sin\theta $ となる.また $ \alpha+\beta=2c $ である.
これを用いて,数列 $ \{s_n\} $ を
\[
s_n=\dfrac{y_n-\beta}{y_n-\alpha}
\]
で定義する.このとき,
\begin{eqnarray*}
s_{n+1}&=&\dfrac{y_{n+1}-\beta}{y_{n+1}-\alpha}
=\dfrac{2c-\frac{1}{y_n}-\beta}{2c-\frac{1}{y_n}-\alpha}=\dfrac{\alpha-\frac{1}{y_n}}{\beta-\frac{1}{y_n}}\\
&=&\dfrac{\alpha y_n-1}{\beta y_n-1}=\dfrac{\alpha}{\beta}\cdot\dfrac{y_n-\beta}{y_n-\alpha}=\dfrac{\alpha}{\beta}\cdot s_n
\end{eqnarray*}
となるので,
\[
s_n=\left(\dfrac{\alpha}{\beta} \right)^{n-1}s_1
=\left(\dfrac{\alpha}{\beta} \right)^{n-1}\dfrac{2c-\beta}{2c-\alpha}
=\left(\dfrac{\alpha}{\beta} \right)^n
\]
である.よって,
\[
\dfrac{y_n-\beta}{y_n-\alpha}=\dfrac{\alpha^n}{\beta^n}
\]
これを逆に解いて,
\[
y_n=\dfrac{\beta^{n+1}-\alpha^{n+1}}{\beta^n-\alpha^n}
\]
である.ド・モアブルの定理から
\begin{eqnarray*}
y_n&=&\dfrac{\cos(n+1)\theta+i\sin(n+1)\theta-\cos(n+1)\theta+i\sin(n+1)\theta}{\cos n \theta+i\sin n \theta-\cos n \theta+i\sin n \theta}\\
&=&\dfrac{\sin(n+1)\theta}{\sin n \theta}=\dfrac{\sin n\theta\cos\theta+\cos n\theta\sin\theta}{\sin n \theta}
=\cos\theta+\dfrac{\sin\theta}{\tan n\theta}
\end{eqnarray*}
となる.ここで, $ \theta=1(ラジアン) $ にとり, $ c=\cos 1 $ とする.このとき,与えられた $ M $ に対して
\[
|y_N|=\left|\cos 1+\dfrac{\sin 1}{\tan N} \right| >M
…①
\]
となる $ N $ が存在することを示す.
$ 0< \cos 1< 1 $ なので, $ \tan n $ の正負にかかわらず
$ \left|\dfrac{\sin 1}{\tan N} \right| >M+1 $ であればよい.つまり
\[
\dfrac{\sin 1}{M+1}>|\tan N|
\]
となればよい. $ \tan \epsilon=\dfrac{\sin 1}{M+1} $ とおく.
$ 0< \epsilon< \dfrac{\pi}{2} $にとる.
ここで,自然数 $ n \ (n\geqq 4)$ に対して,
\[
n=q_n\pi +r_n\ (0< r_n< \pi)
\]
となる正整数 $ q_n $ と実数 $ r_n $ をとる. $ \pi $ が無理数なので,
数列 $ \{r_n\} $ の項はすべて無理数でかつ異なり,区間 $ (0,\ \pi) $ に属している.
したがって少なくとも一組
\[
|r_m-r_{m+l}|< \epsilon
\]
となるものが存在する.
\[
m=q_{m}\pi +r_{m},\
m+l=q_{m+l}\pi +r_{m+l}
\]
より
\[
l=\left(q_{m+l}-q_{m} \right)\pi+r_{m+l}-r_m
\]
である. $ \tan \left(q_{m+l}-q_{m} \right)\pi=0 $ なので,
\[
|\tan l|=\tan |l|=\tan\left|r_{m+l}-r_m\right|<\tan \epsilon
\]
したがって, $ N=|l| $ が条件 $ ① $ を満たす.
$ q=y_N $ とおけば, $ q $ が条件を満たす不都合な初項である.
つまり,命題 (P) が成り立つような実数 $ c $ が $ 0< c< 1 $ の範囲に存在した.