神戸大理系2番解答
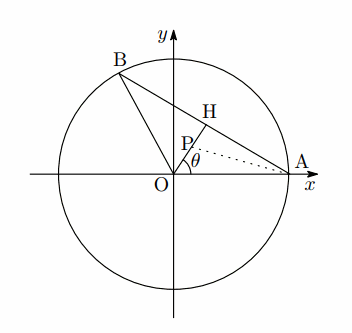
(1) $ \mathrm{O} $ から辺 $ \mathrm{AB} $ に垂線を引き,交点を $ \mathrm{H} $ とする.
$ \bigtriangleup \mathrm{OAB} $ は二等辺三角形なので,内接円の中心 $ \mathrm{P} $ は $ \mathrm{OH} $ 上にある.
$ \angle \mathrm{AOP}=\dfrac{1}{2}\angle \mathrm{AOB}=\theta $ である.
$ \mathrm{OH}=\cos\theta $ である.
線分 $ \mathrm{AP} $ は $ \angle \mathrm{OAH} $ を2等分するので,
\[
\mathrm{OP}:\mathrm{PH}=\mathrm{AO}:\mathrm{AH}=1:\sin\theta
\]
である.
よって, \[ \mathrm{OP}=\dfrac{1}{1+\sin\theta}\mathrm{OH}=\dfrac{\cos\theta}{1+\sin\theta} \] この結果, \[ \overrightarrow{\mathrm{OP}}=\dfrac{\cos\theta}{1+\sin\theta}\left(\cos\theta,\ \sin\theta \right) =\left(1-\sin\theta,\ \dfrac{\cos\theta\sin\theta}{1+\sin\theta} \right) \] となる.
(2)
$ 0<\theta<\dfrac{\pi}{2} $ において $ \sin\theta $ は単調増加関数であるから,
点 $ \mathrm{P} $ の $ x $ 座標を $ X $ とすると, $ X=1-\sin\theta $ は単調減少関数である.
$ \theta:0 \to \dfrac{\pi}{2} $ のとき, $ X:1 \to 0 $ で,
この範囲で $ X $ は単調である.よって,
$ D $ を $ x $ 軸のまわりに1回転させてできる立体の体積を $ V $ とすると,
\[
V=\int_0^1\pi Y^2\,dX
\]
である.ここで,
\begin{eqnarray*}
Y^2
&=&\dfrac{\cos^2\theta\sin^2\theta}{(1+\sin\theta)^2}
=\dfrac{(1-\sin\theta)\sin^2\theta}{1+\sin\theta}\\
&=&\dfrac{X(1-X)^2}{2-X}=-X^2-1+\dfrac{2}{2-X}
\end{eqnarray*}
よって,
\begin{eqnarray*}
V
&=&\pi\int_0^1\left(-X^2-1+\dfrac{2}{2-X} \right)\,dX\\
&=&\pi\biggl[-\dfrac{X^3}{3}-X-2\log\left|2-X\right|\biggr]_0^1
=\pi\left(2\log 2-\dfrac{4}{3} \right)
\end{eqnarray*}