特色入試総人理系1番解答
(1) $ \displaystyle f_N(x)=\sum_{n=0}^N\dfrac{s(2^nx)}{2^n}\quad (0\leqq x \leqq 1) $ とおく. \[ f_N(0)=f_N(1)=0,\ \quad f_N\left(\dfrac{1}{2} \right)=s\left(\dfrac{1}{2} \right)+\dfrac{s(1)}{2}+\dfrac{s(2)}{2^2}+\cdots =s\left(\dfrac{1}{2}\right) =\dfrac{1}{2} \] である. ここで \[ s(x)= \left\{ \begin{array}{ll} x&\left(0\leqq x \le\dfrac{1}{2}\right)\\ 1-x&\left(\dfrac{1}{2}\leqq x \leqq 1\right) \end{array} \right. \] である. $ y=s(2^nx) $ のグラフは $ y=s(x) $ のグラフを $ x $ 方向に $ \dfrac{1}{2^n} $ に縮めたものであるから, それぞれ次のようになる.
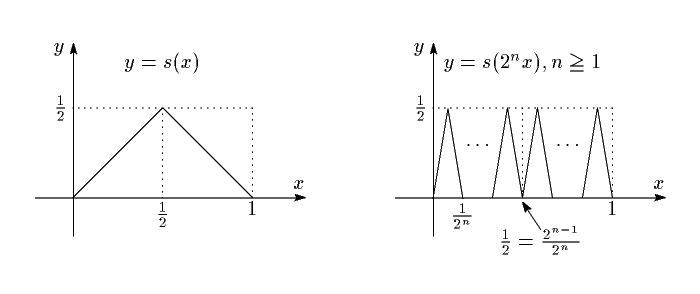
$ 0\leqq n\leqq N $ に対して $ y=s(2^nx) $ のグラフは直線 $ x=\dfrac{1}{2} $ に関して対称である.
よって, $ y=f_N(x) $ のグラフも直線 $ x=\dfrac{1}{2} $ に関して対称である.
$ y=f_N(x) $ のグラフの区間 $ 0\leqq x \leqq \dfrac{1}{2} $ に対応する部分と $ x $ 軸で囲まれた領域の面積を $ S $ とおく.
\[
S=\int_0^{\frac{1}{2}}f_N(x)\,dx=
\sum_{n=0}^N\int_0^{\frac{1}{2}}\dfrac{s(2^nx)}{2^n}\,dx
\]
上のグラフよりわかるように, $ \displaystyle
\int_0^{\frac{1}{2}}s(2^nx)\,dx=\dfrac{1}{8} $ となる.よって,
\[
S=\dfrac{1}{8}\sum_{n=0}^N\dfrac{1}{2^{n}}
=\dfrac{1}{8}\cdot\dfrac{1-\left(\dfrac{1}{2}\right)^{N+1}}{1-\dfrac{1}{2}}
=\dfrac{1}{4}\left(1-\dfrac{1}{2^{N+1}}\right)
\]
である.
次に面積が $ S $ となるこの領域を $ x=\dfrac{1}{2} $ を軸に回転した回転体の体積を求める.
重心の $ x $ 座標が求まれば,パップス・ギュルダンの定理より体積を求めることができる.
重心の $ x $ 座標を $ r $ とする.
\[
r=\dfrac{1}{S}\int_0^{\frac{1}{2}}f_N(x)x\,dx
=\dfrac{1}{S}\int_0^{\frac{1}{2}}\left\{\sum_{n=0}^N\dfrac{s(2^nx)}{2^n}\right\}x\,dx
=\dfrac{1}{S}\sum_{n=0}^N\dfrac{1}{2^n}\int_0^{\frac{1}{2}}s(2^nx)x\,dx
\]
ここで, $ \displaystyle \int_0^{\frac{1}{2}}s(2^nx)x\,dx $ は, $ y=s(2^nx) $ で定まる区間 $ 0\leqq x \leqq \dfrac{1}{2} $ の面積と重心の $ x $ 座標の積である.
その値は, $ n=0 $ のときは次図のように $ \dfrac{1}{8}\cdot\dfrac{1}{3} $ であり,
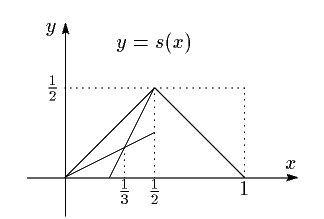
$ n\geqq 1 $ のときは明らかに $ \dfrac{1}{8}\cdot\dfrac{1}{4} $ である.よって, \[ rS=\sum_{n=0}^N\dfrac{1}{2^n}\int_0^{\frac{1}{2}}s(2^nx)x\,dx =\dfrac{1}{24}+\dfrac{1}{32}\left(\sum_{n=1}^N\dfrac{1}{2^n} \right) =\dfrac{1}{24}+\dfrac{1}{32}\left(1-\dfrac{1}{2^N}\right) \] 重心の $ x $ 座標と回転軸との距離は $ \dfrac{1}{2}-r $ なので, パップス・ギュルダンの定理よりブラマンジエの体積 $ V_N $ は \begin{eqnarray*} V_N&=&2\pi \left(\dfrac{1}{2}-r \right) S=\pi(S-2rS)\\ &=&\pi\left\{\dfrac{1}{4}\left(1-\dfrac{1}{2^{N+1}}\right) - \dfrac{1}{12}-\dfrac{1}{16}\left(1-\dfrac{1}{2^N}\right)\right\} \end{eqnarray*} である.
(2)
\[
\lim_{N\to \infty}V_N=
\pi\left(\dfrac{1}{4}-\dfrac{1}{12}-\dfrac{1}{16}\right)=\dfrac{5\pi}{48}
\]
である.
※
重心という概念は物理学のものである.だから,数学では本問中の第2の命題を重心の定義としてもよい.
重心の定義式は
\[
\left(
\dfrac{1}{S}\int_a^b\left(\psi(x)-\phi(x)\right)x\,dx,\
\dfrac{1}{S}\int_a^b\dfrac{\psi(x)+\phi(x)}{2}\cdot \left(\psi(x)-\phi(x)\right)\,dx\right)
\]
と書ける.
重心の $ x $ 座標を $ X $ とすると,
\[
SX=\int_a^b\left(\psi(x)-\phi(x)\right)x\,dx
\]
となる.右辺は $ x $ 方向の重みつき平均である.
$ y $ 座標については, $ y $ 方向の中点の重みつき平均となり,
物理的な意味が分かる.
また,回転体の体積は,軸からの距離を $ x $ とおけば
\[
\int_a^b2\pi\left(\psi(x)-\phi(x)\right)x\, dx
\]
となる.論証は,定積分の定義と同様の議論を経る必要があるが,意味は明確である.
そして,これは重心の移動距離 $ 2\pi X $ の $ S $ 倍である.
これが,パップス・ギュルダンの定理である.