東大理科第2問解答
$ S(X)=\bigtriangleup \mathrm{ABX}+
\bigtriangleup \mathrm{BCX}+
\bigtriangleup \mathrm{CAX} $ とおく.
$ \mathrm{X} $ が $ \bigtriangleup \mathrm{ABC} $ の周か内部にあるときは
$ S(X)=1 $ である.これは条件をみたさない.
よって, $ \mathrm{X} $ は $ \bigtriangleup \mathrm{ABC} $ の外部にある.
$ \bigtriangleup \mathrm{ABC} $ の外部は,3直線 $ \mathrm{AB,BC,CA }$ で6個の領域に分けられる.
$ \mathrm{X} $ が $ \bigtriangleup \mathrm{ABC} $ の辺を共有する領域にあるときと,
$ \mathrm{X} $ が $ \bigtriangleup \mathrm{ABC} $ の辺を共有しない領域にあるときに分ける.
i)
$ \mathrm{X} $ が $ \bigtriangleup \mathrm{ABC} $ の辺を共有しない領域にあるとき
頂点Aにつながる領域にあるとする.このとき,
$ S(X)=
2\bigtriangleup \mathrm{BCX}-\bigtriangleup \mathrm{ABC} $
より, $ \dfrac{3}{2}\leqq \bigtriangleup \mathrm{BCX}\leqq 2 $
である.
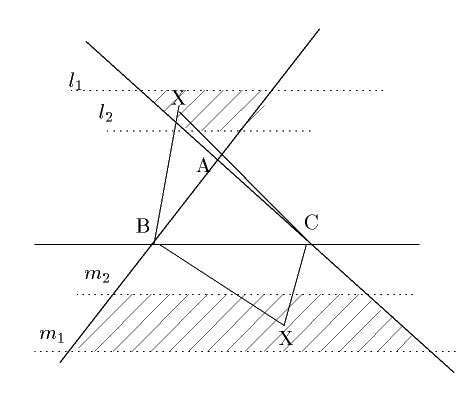
辺 $ \mathrm{BC} $ に対する高さを考え, $ \mathrm{BC} $ からの距離がBCに対する高さの2倍にある直線 $ l_1 $ と,
1の距離にある直線 $ l_2 $ をとる.
$ \mathrm{X} $ はこの2直線と直線 $ \mathrm{AB} $ , $ \mathrm{AC} $ で囲まれた領域にある.
この面積は
$ 1^2-\left(\dfrac{1}{2} \right)^2=\dfrac{3}{4} $ である.
ii)
$ \mathrm{X} $ Xが $ \bigtriangleup \mathrm{ABC} $ の辺を共有する領域にあるとき
辺 $ \mathrm{BC} $ を共有する領域にあるとする.このとき,
$ S(X)=
2\bigtriangleup \mathrm{BCX}+\bigtriangleup \mathrm{ABC} $ より,
$ \dfrac{1}{2}\leqq \bigtriangleup \mathrm{BCX}\leqq 1 $ である.
辺 $ \mathrm{BC} $ に対する高さを考え, $ \mathrm{BC} $ からの距離が $ \mathrm{BC} $ に対する高さと
同じ距離にある直線 $ m_1 $ と, $ \dfrac{1}{2} $ の距離にある直線 $ m_2 $ をとる.
$ \mathrm{X} $ はこの2直線と直線 $ \mathrm{AB} $ , $ \mathrm{AC} $ で囲まれた領域にある.
この面積は
$ 2^2-\left(\dfrac{3}{2} \right)^2=\dfrac{7}{4} $ である.
これらは長さの比のみで決まるので,領域の他の部分にあっても同じである.
よって,Xの動きうる範囲の面積は
\[
\dfrac{3}{4}\times 3+\dfrac{7}{4}\times 3=\dfrac{15}{2}
\]
である.