東大理科第5問解答
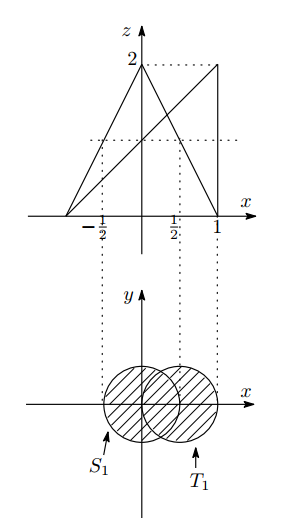
(1) 直円錐 $ S $ と斜円錐 $ T $ を $ z=t\ (0\leqq t \leqq 2) $ での断面の円を それぞれ $ S_t $ , $ T_t $ とおく. 比例から $ S_1 $ および $ T_1 $ は半径 $ \dfrac{1}{2} $ の円であり, その中心は $ (0,\ 0,\ 1) $ と $ \left(\dfrac{1}{2},\ 0,\ 1\right) $ であるから,それぞれ次図の斜線部分である.
(2) 点 $ \mathrm{P} $ が $ S $ を動くとき,線分 $ \mathrm{AP} $ が通過する領域を $ D $ とする. $ D $ はまた,直円錐の底面を $ S_0 $ から $ S_2 $ まで移動させたとき, その底面と頂点 $ \mathrm{A} $ でできる斜円錐の通過領域でもある.
直円錐を半径を $ z=t $ で切った断面の円の半径を $ r $ とすると, $ 2:1=2-t:r $ より, $ r=1-\dfrac{t}{2} $ である.
次に,底面の $ z $ 座標が $ u $ であるとき,この $ 1-\dfrac{u}{2} $ を半径とする円と 頂点 $ \mathrm{A} $ でできる斜円錐を考える.
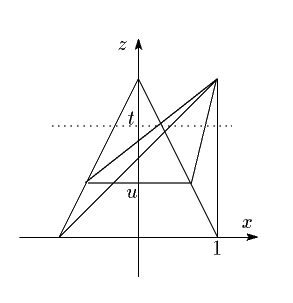
この斜円錐を $ z=t $ 平面で切った断面の円の半径を $ s $ とすると \[ 1-\dfrac{u}{2}:s=2-u:2-t \] なので, $ s=1-\dfrac{t}{2} $ となり,半径は変わらない.
したがって $ D $ を $ z=t $ で切った断面は,円 $ T_t $ から同じ半径の円が $ S_t $ まで動いた通過領域になる.
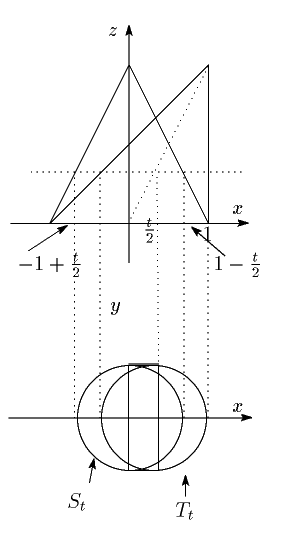
また $ T_t $ の中心の $ x $ 座標は $ \dfrac{t}{2} $ である.
したがってこの通過領域を,2つの半円の和と長方形に分けることにより,
断面積は
\[
\pi\left(1-\dfrac{t}{2} \right)^2+\dfrac{t}{2}\cdot2\left(1-\dfrac{t}{2} \right)
=\dfrac{\pi}{4}(2-t)^2+\dfrac{t(2-t)}{2}
\]
となる.
よってその体積 $ V $ は
\begin{eqnarray*}
V&=&\int_0^2\left\{\dfrac{\pi}{4}(2-t)^2+\dfrac{t(2-t)}{2} \right\}\,dt\\
&=&\biggl[\dfrac{\pi}{12}(t-2)^3+\dfrac{-t^3+3t^2}{6}\biggr]_0^2\\
&=&\dfrac{2}{3}(\pi+1)
\end{eqnarray*}