----------------------------------
切断を使って次のように積の定義の改良をしたいのですが.
命題 ![]() の切断で0を含まない組を
の切断で0を含まない組を
![]() ,
,![]() のそれを
のそれを![]() とし,
とし,
![]() ,
,
![]() の積
の積![]() の集合を
の集合を
![]() とすると,それはある切断の0を含まないほうの組である.
とすると,それはある切断の0を含まないほうの組である.
この切断をもって積
![]() を定義したいのですが,成り立ちますか?
を定義したいのですが,成り立ちますか?
----------------------------------
どのような方法をとるか.当時,インターネットが普及しはじめ,メーリングリストが利用できるようになっていました.各自がメールアドレスを登録すれば,サーバーに送ったメールが登録者全員に配送される,それだけの仕組みです.
数学関係の掲示板などで呼びかけ,本誌の「数セミ掲示板」にも載せてもらいました.10人も集まればはじめようと考えていました.しかし反響は予想以上で,2000年のうちに70人,その後,毎年新しい人が参加し,現在は400人を超える人が登録しています.
----------------------------------
切断を使って次のように積の定義の改良をしたいのですが.
命題 ![]() の切断で0を含まない組を
の切断で0を含まない組を
![]() ,
,![]() のそれを
のそれを![]() とし,
とし,
![]() ,
,
![]() の積
の積![]() の集合を
の集合を
![]() とすると,それはある切断の0を含まないほうの組である.
とすると,それはある切断の0を含まないほうの組である.
この切断をもって積
![]() を定義したいのですが,成り立ちますか?
を定義したいのですが,成り立ちますか?
----------------------------------
これで俄然,議論が盛り上がりました.定義の内容に対する疑問や意見,このような定義を考えること自体に対する議論などが飛び交い,議論が錯綜してきたので,途中でまとめを入れました.
----------------------------------
普通の解析の教科書は次の3項を「実数の公理」として掲げ,この公理を満たす集合
![]() を実数とします.
を実数とします.
そこで,実数論は有理数体
![]() の存在を前提に次のことを証明します.
の存在を前提に次のことを証明します.
『解析概論』は解析学の入門書として,実数論は折衷的です.ですから,連続性の公理相互の関係や,構成方法と公理の関係を解明することはそれほど重視されていません.
有理数
![]() の切断の集合
の切断の集合
![]() に体の構造を入れるにあたって,積の定義と積に関する計算法則成立の証明を,『解析概論』のように級数でするのではなく,切断でやってみようというのが Kさんの問題提起です.
に体の構造を入れるにあたって,積の定義と積に関する計算法則成立の証明を,『解析概論』のように級数でするのではなく,切断でやってみようというのが Kさんの問題提起です.
----------------------------------
実際にKさんの定義を実行して,報告もしました.
----------------------------------
Kさんの定義が新たな切断を定めているかの検証をしてみました.ただし切断で定義された実数
![]() には,有理数
には,有理数
![]() がすでに埋め込まれ,
がすでに埋め込まれ,
![]() の全順序と整合する全順序と加法はすでに定義できているとします.切断が有理数のときは
の全順序と整合する全順序と加法はすでに定義できているとします.切断が有理数のときは
![]() と
と
![]() の2つの切断を同一視し,具体的に考えるときは境界は上の集合に入れることにします.
の2つの切断を同一視し,具体的に考えるときは境界は上の集合に入れることにします.
![]() ,
,
![]() とする.以下集合はすべて
とする.以下集合はすべて
![]() の部分集合である.
の部分集合である.
![]() ,
,![]() のとき.
のとき.
![]() ,
,
![]() (以下,全順序は定義できているので有理数と無理数でも不等式は意味がある).
(以下,全順序は定義できているので有理数と無理数でも不等式は意味がある).
Kさんの定義した
![]() に対し,
に対し,
![]() とおく.
とおく.![]() の補集合を
の補集合を![]() とする.
とする.
![]() ,
,
![]() に対し
に対し![]() を示せばよい.
を示せばよい.
![]() となったとする.
となったとする.
![]() ,
,
![]() として
として![]() とする.
とする.
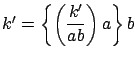 において,
において,![]() より
より
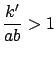 .よって
.よって
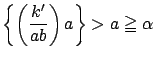 となる.つまり
となる.つまり
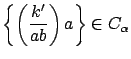 .
.
![]() が
が
![]() と
と![]() の要素の積で表せたので,
の要素の積で表せたので,![]() に矛盾する.よって
に矛盾する.よって![]() .つまり
.つまり![]() は切断である.(
は切断である.(![]() ,
,![]() 以外の場合は略します)
以外の場合は略します)
たしかに切断が定義できています.結合法則,分配法則の確認は可能であるようですが,実行はできませんでした.
----------------------------------
また,いわゆる「アルキメデスの原則」は『解析概論』では歴史に従いアルキメデスの求積法のところに書かれています.私は,実数論を議論するなら最初に議論すべきと考えたので,次の問題を提起しました.
----------------------------------
これに対してもいろいろな議論が続き,しばらくおいてGさんからつぎの返答がありました.
----------------------------------
アルキメデスの原則は『解析概論』に書かれている証明の中では,
(IV)区間縮小法 ![]() (I)Dedekind の定理
(I)Dedekind の定理
の証明において使われています.また,(IV)区間縮小法以外の公理,(I)Dedekind の定理(切断),(II)Weier- strass の定理(上限・下限),(III)有界な単調数列の収束からは「アルキメデスの原則」が導かれることを確認しました.
----------------------------------
一応これで議論は落ちつきました.解析の準備として実数の構造を学ぶはずだったのが,「実数論の構造」に深入りして議論がやや難解になりました.進行役として,解決したことと未解決のことを確認しつつ2章に進み,計算にも力を入れるようにしました.こうしたやりとりを重ねながら章末問題をすべて解いていったのです.2000年6月から2002年3月にかけ何とか読み通しました.
これらの記録はすべて現在もウェブ内で公開されています.興味をもたれた方は登録のうえご覧ください.この読書会は,「終わった議論をいつ蒸し返してもよい」ということでやってきています.新たに読まれた方からの疑問・反論・誤りの指摘,大いに歓迎です.
最近になっても「学生時代,何回もつまづいて,あきらめてしまった.人生の終わりに近づき,一歩でも前進したくて『解析概論』に挑戦します」と自己紹介をして登録する人がいます.まことに『解析概論』は日本の数学書の古典だと認識を新たにしました.
----------------------------------
最初の頃,数学書の読み方がつかめず,テキストをなぞることから始めた記憶があります.計算中心の数学にばかり接していた学生時代に身につけた,自分流の読み方でも理解することができると,徐々に自信が出てきました.抽象化・一般化の意義も,計算で確認しようとするとよく理解できることがあります.代数多様体の射影的集合を定義するイデアルが素イデアルであることの証明で,計算してもラチが開かず,視点を変えて代数的に解いたら簡単に解け,よく理解できた経験もあります.
数学の本を一人で読むのはつらいことです.読書会は,わからなければ聞くことができます.同時に,他人に理解させようと整理する過程で,こちらがわかってくることがよくあります.
----------------------------------
ここに,数学の専門家でない社会人にとっての,数学書を読む意義と楽しみがあります.
『曲線と曲面の微分幾何』を読む頃は仕事のほうが忙しくなり,時間を割くことができなくなりました.私は当分休みたいと思い,次の呼びかけがなかなかできませんでした.しかし,読書会を中断すると何か落ち着かない.ここは原点にかえって,自分が読みたい本を読もう.その頃, 『数論I――Fermat の夢と類体論』(加藤和也,黒川信重,斎藤毅著,岩波書店)が出版されました.青空学園数学科には『数論初歩』というタイトルで有理整数論の入門を用意しています.それ以外の準備として,『ガロア理論』(J.ロットマン著,関口次郎訳,シュプリンガー・フェアラーク東京),『代数幾何入門』(上野健爾著,岩波書店)を読み,続いて『数論I』を読もうと提案しました.2005年の1月,半年ほど休んだ後のことです.
2006年に入り,いよいよ『数論I』に進みました.この段階になると,さすがに投稿者は多くありません.草の根のささやかな取り組みですが,楽しみながら,ゆっくりと進んでいきます.あちこちにいろいろな読書会ができて,互いに助けあえればいいと思います.