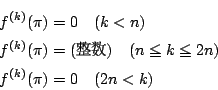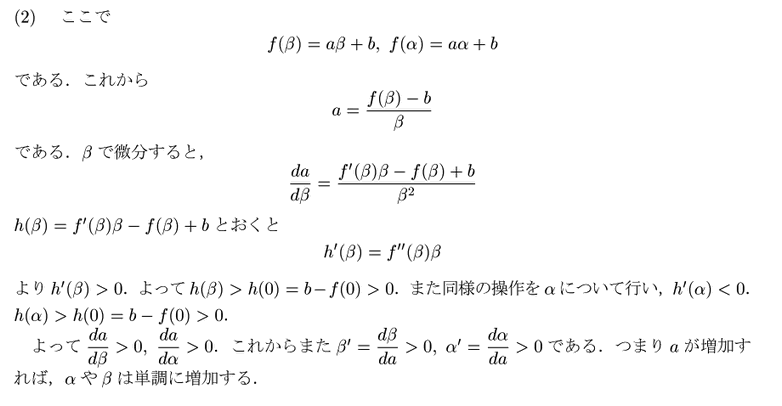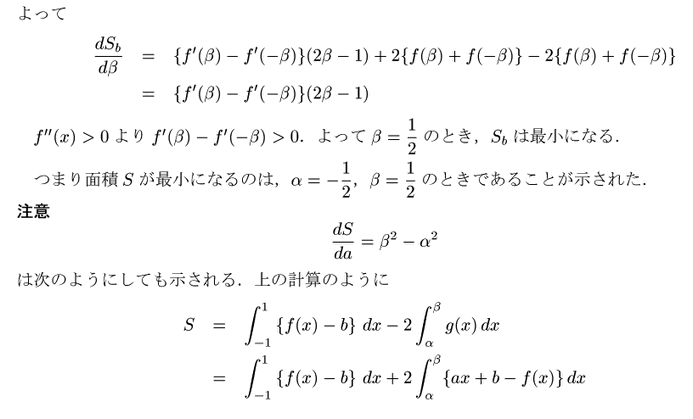1.![]() ,
,![]() の最高次数の係数を
の最高次数の係数を![]() と
と![]() とする.
とする.
![]() とする.
このとき
とする.
このとき![]() は
は![]() 次以下の整式である.したがって
次以下の整式である.したがって
![]()
となる.
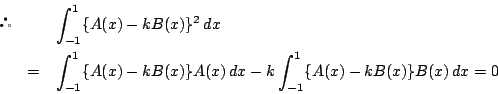
これから関数![]() は区間
は区間![]() でつねに0である.
ところが
でつねに0である.
ところが![]() は整式なので,すべての
は整式なので,すべての![]() で
で![]() .
つまり
.
つまり![]() と表された.
と表された.
2.次のように順次部分積分を行う.![]() は
は![]() 次式なので
次式なので![]() である.
である.
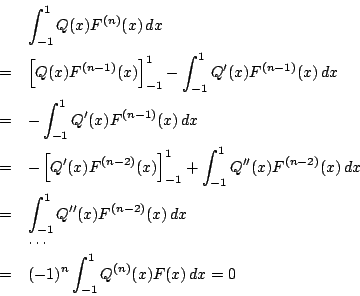
3.
![]() とおく.
とおく.
![]() の
の![]() に対して
に対して
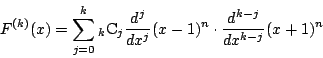
となる.ゆえに
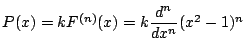 と表される.
と表される.
4.
1.![]() ,
,![]() の最高次数の係数を
の最高次数の係数を![]() と
と![]() とする.
とする.
![]() とする.
このとき
とする.
このとき![]() は
は![]() 次以下の整式である.したがって
次以下の整式である.したがって
![]()
となる.
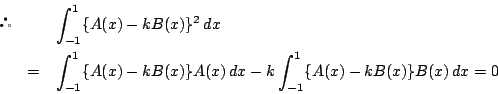
これから関数![]() は区間
は区間![]() でつねに0である.
ところが
でつねに0である.
ところが![]() は整式なので,すべての
は整式なので,すべての![]() で
で![]() .
つまり
.
つまり![]() と表された.
と表された.
2.次のように順次部分積分を行う.![]() は
は![]() 次式なので
次式なので![]() である.
である.
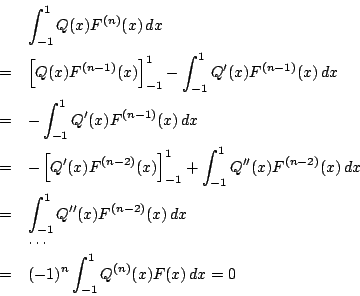
3.
![]() とおく.
とおく.
![]() の
の![]() に対して
に対して
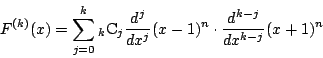
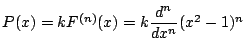 と表される.
と表される.
4.

5.![]() を
を![]() と書く.
と書く.
![]() ,
,
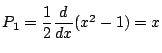 .(4)の漸化式から
.(4)の漸化式から
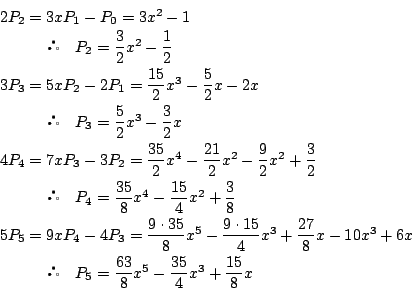
6.
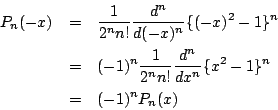
次に
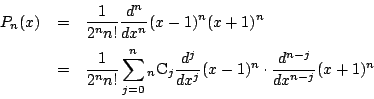
![]() の項は
の項は
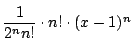 ,
,
![]() の項は
の項は
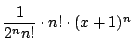 .
.
![]() の項は,
の項は,![]() を因数にもつ.
を因数にもつ.
7.数学的帰納法で示す.
![]() のとき.
のとき.
![]() の根は
の根は![]() ,
, ![]() の根は
の根は
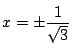 より成立.
より成立.
![]() のとき成立してるとする.
のとき成立してるとする.
つまり,
![]() より
より
![]() .
漸化式から
.
漸化式から
![]() なので
なので
一方,
![]() と
と
![]() は異符号なので,
は異符号なので,
![]() より
より
あわせて![]() 個の根が
個の根が
![]() の間にある.
の間にある.
次に
![]() で
で
![]() .また
.また![]() と
と
![]() は同符号.漸化式から
は同符号.漸化式から
![]() .
.
これで![]() の
の![]() 個の根がすべて尽くされた.
個の根がすべて尽くされた.
つまり![]() でも成立した.
でも成立した.
したがって,![]() の根はすべて実数で,
の根はすべて実数で,![]() と
と![]() の間にあり,重解ではなく,
の間にあり,重解ではなく,
![]() の根で分離されることが示された.
の根で分離されることが示された.
8.最高次数の係数が![]() と一致する任意の
と一致する任意の![]() 次多項式
次多項式 ![]() に対して
に対して
![]() は
は![]() 次以下の整式になる.これを
次以下の整式になる.これを![]() とおく.つまり
とおく.つまり
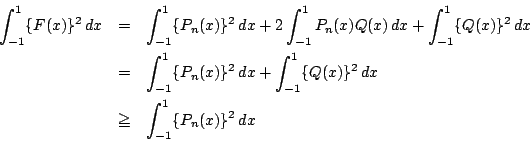
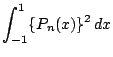 .
.
この値を計算する.
まず
![]() が
が![]() 次以下となる
次以下となる![]() を求める.
を求める.![]() の
の![]() の係数は
の係数は
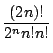 であり,
であり,
![]() の
の![]() の係数は
の係数は
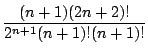 である.
である.
したがって
一方
したがって
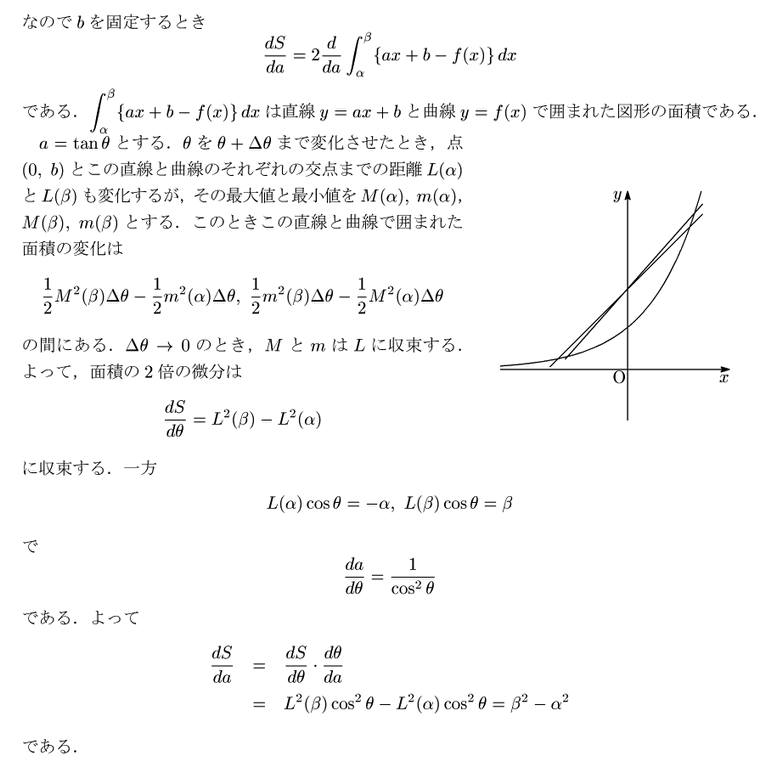
9.(この部分だけ![]() 次線形代数を使う.高校範囲を超える.)
次線形代数を使う.高校範囲を超える.)
とおく.
一方
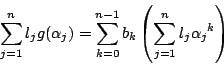
これが任意の
![]() について成立するために
について成立するために
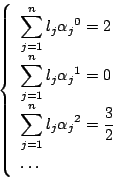
となるように
![]() を決めればよい.
を決めればよい.
ヴァンデルモンドの行列式より
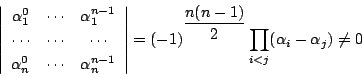
なのでこれは可能である.
10.![]() を
を![]() で割り,商を
で割り,商を![]() ,余りを
,余りを![]() とおく.
とおく.
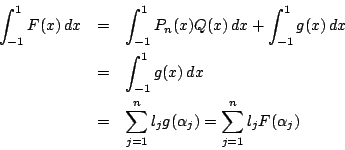
![\begin{eqnarray*}
I_n&\leq&\int_0^{\pi}\dfrac{1}{n!}{\pi}^n q^n\,dx \\
&=&\df...
...{n!}\left[{\pi}^n q^n x\right]_0^{\pi}=\dfrac{(\pi q)^n}{n!}\pi
\end{eqnarray*}](images/img718.gif)
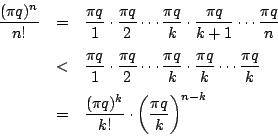
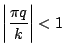 より
より
![\begin{eqnarray*}
I_n&=&\int_0^{\pi}f(x)\sin x\,dx \\
&=&\left[-f(x)\cos x\ri...
...=&\left[-f(x)\cos x\right]_0^{\pi}-\int_0^{\pi}f''(x)\sin x\,dx
\end{eqnarray*}](images/img727.gif)
![\begin{displaymath}
I_n=\left[\sum_{k=0}^n(-1)^{k+1}f^{(2k)}(x)\cos x\right]_0^{\pi}
+(-1)^n\int_0^{\pi}f^{(2n+1)}(x)\cos x\,dx
\end{displaymath}](images/img728.gif)
![\begin{displaymath}
f^{(2n+1)}(x)=0\qquad∴\quad I_n
=\left[\sum_{k=0}^n(-1)^{k+1}f^{(2k)}(x)\cos x\right]_0^{\pi}
\end{displaymath}](images/img730.gif)
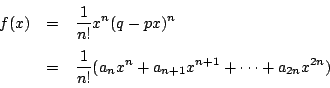
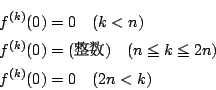
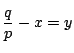 とおくと
とおくと
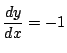 なので,
なので,