k連勝している人が先頭にいるときのm番目にいる人の
優勝する確率をPk,mとおきます.
(
![]() )
)
![]() を求めることが
最終目標です.
を求めることが
最終目標です.
(n-1)連勝しているとき 先頭の人が優勝しているのだから
が成り立ちます.
次に,k連勝
![]() しているとき,
先頭の二人が勝負することを考えましょう.
しているとき,
先頭の二人が勝負することを考えましょう.
先頭にいる人は,1/2の確率で(k+1)連勝するか, 1/2の確率で負けるかのどちらかです.
ですから,
同様に,2番目の人は
3番目以降の人は,自らは勝負をしませんが ひとつ順番があがることに注意しましょう.
ここで得た式を 並べておきましょう.
式を与えられれば解けるはずですが 実際に解くのはかなり難しくなります.
ここでは,おなじみの行列を用いる方法, 式変形だけで解く方法を紹介します.
この方法は大学生で習う余因子行列や行列式の 基礎的な知識があれば理解できるはずです.(多分..)
漸化式より
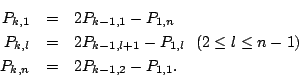
このとき,
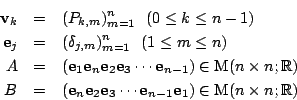
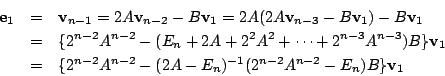
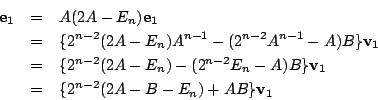
まず M の形を調べる.
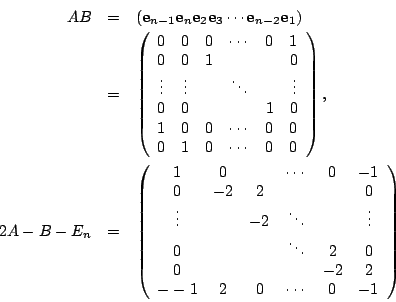
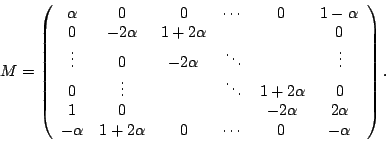
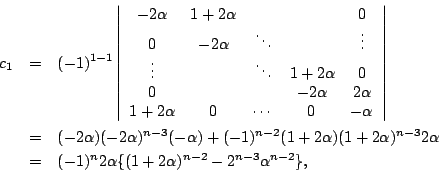
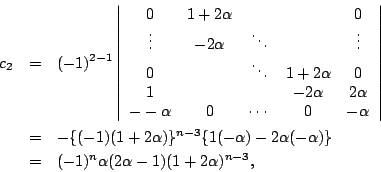
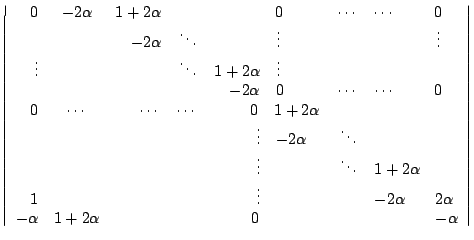
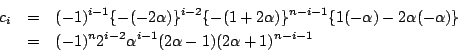
![\begin{eqnarray*}c_n&=&(-1)^{n-1}
\left\vert
\begin{array}{ccccc}
0&-2\alpha&1+2...
...a)^{n-2}]\\
&=&(-1)^n\{2^{n-2}\alpha^{n-1}
-(1+2\alpha)^{n-2}\}
\end{eqnarray*}](images/img30.gif)
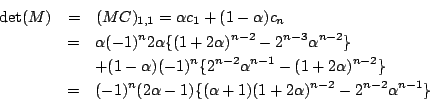
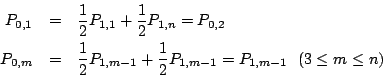
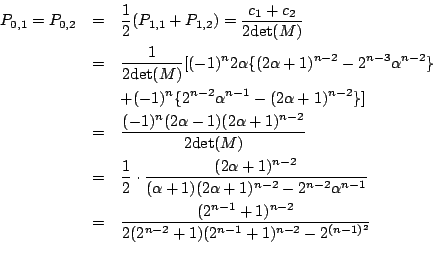
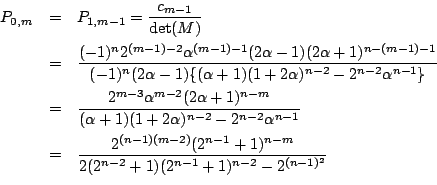
![]()
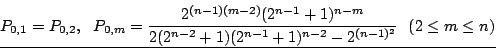
これ以降は高校生にも理解可能です. 誘導をつければ難しめの入試問題とでもいった感じになります.
式だけ与えてやれというのは,, どの変数が重要かということを理解していないと どうどうめぐりの式を量産して投げ出してしまいそうです. 私自身 多大な時間を費やしてしまったので 高校生では,,, いや,道具を知らない高校生こそができるに違いない.
に注意します.作戦としては, 「各P1,mをひとつの文字で表す」 ことを目指します.
まずP1,1をP1,nを用いて表すことを考えます.
(1)を繰り返し用いることによって
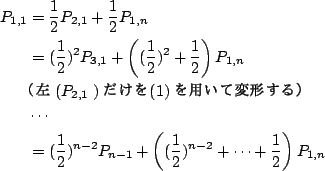
(4)より Pn-1,1=1であるから
次に,
![]() を調べます.ここでは
でてきた式を
(3)を用いて一番左だけを変形していきます.
また,(4)を効果的に用いている
ことに注意しましょう.
を調べます.ここでは
でてきた式を
(3)を用いて一番左だけを変形していきます.
また,(4)を効果的に用いている
ことに注意しましょう.
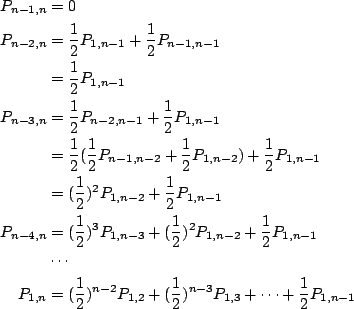
まとめて書いておくと,
![]() に対して
に対して
あるいは
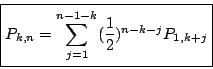
である.
ここで
とおくと,
が成り立つ.
一方,
![]() に対しても同様の操作を行う.
に対しても同様の操作を行う.
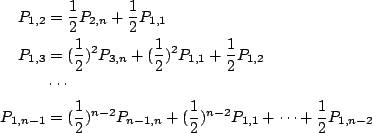
まとめて書いておくと,
![]() に対して
に対して
あるいは
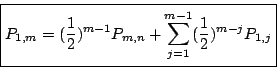
である.
よって,(8)より
(8)より
![]() に対して,
に対して,
が成り立つ.
これで,最初に掲げた作戦はほぼ終了しました. これを(7)に代入してP1,nをP1,2で表すことができます.
さらに,(6)によってP1,1をP1,2で 表すことができます.
したがって,(5)に代入することによって P1,2が得られます.
したがって,
![]() を
すべて求めることができます.
を
すべて求めることができます.
よって,
![]() を求めることができます.
を求めることができます.
(詳しくは,後で書く.)