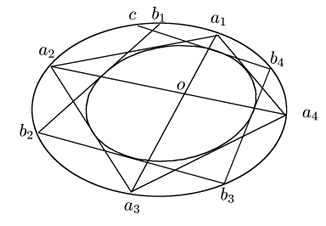
命題83によって
三角形![]() と三角形
と三角形![]() に内接する円錐曲線
に内接する円錐曲線![]() が存在する.
が存在する.
![]() と
と![]() は
三角形
は
三角形![]() の接点,
の接点,![]() ,
,![]() の接点の5点を共有している.
命題82によって5点を指定すれば円錐曲線は一意に定まるので,
の接点の5点を共有している.
命題82によって5点を指定すれば円錐曲線は一意に定まるので,
![]() である.
である.
よって![]() となり,
任意の点についてそれを頂点の一つとする同様の三角形が存在する.
□
となり,
任意の点についてそれを頂点の一つとする同様の三角形が存在する.
□
命題87.1によって
 は対合をなす.よって命題86によって
3直線
は対合をなす.よって命題86によって
3直線
![]() に代えて
に代えて![]() をとることにより
をとることにより
証明
(1)
![]() の中に異なるものが3個以上ある場合.
の中に異なるものが3個以上ある場合.
![]() と
と![]() の接点を
の接点を![]() とし,
とし,![]() とする.
とする.
![]() と
と![]() ,
,![]() の交点をそれぞれ
の交点をそれぞれ![]() とし,
さらに
とし,
さらに![]() と
と![]() との交点を
との交点を![]() ,
,
![]() と
と![]() との交点を
との交点を![]() とする.
とする.
点![]() は
は![]() 上にないので,曲線束
上にないので,曲線束![]() の要素で,
点
の要素で,
点![]() を通るものが一意に存在する.
これを
を通るものが一意に存在する.
これを![]() とする.
とする.
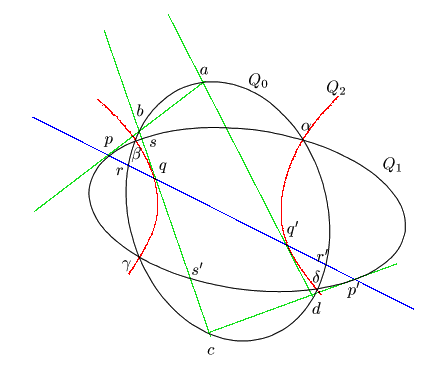 デザルグの対合定理86の証明を
曲線束
デザルグの対合定理86の証明を
曲線束![]() に適用して,三つの点対
に適用して,三つの点対
次に円錐曲線![]() は点
は点![]() で
で![]() ,
,![]() と接することを示す.再びデザルグの対合定理の証明と同様にして
と接することを示す.再びデザルグの対合定理の証明と同様にして
![\begin{eqnarray*}[q,\ c;\ s,\ s']&=&[p'\vee q,\ p'\vee c;\ p'\vee s,\ p'\vee s']...
...ee p';\ p\vee s,\ p\vee s']=
[b,\ q;\ s,\ s']=[q,\ b;\ s',\ s]
\end{eqnarray*}](images/img2516.gif)
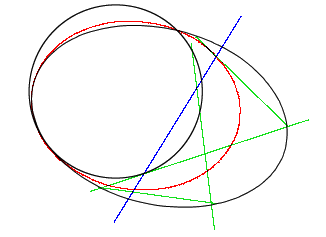 この証明は
この証明は![]() の場合もそのまま通用する.他の2点が一致するときは,
点の名前をつけ替えればよい.
の場合もそのまま通用する.他の2点が一致するときは,
点の名前をつけ替えればよい.
また
![]() に同じものがあるときも証明はそのままでよい.
例えば
に同じものがあるときも証明はそのままでよい.
例えば![]() と
と![]() が3重に接している場合もこの証明の中で示せている.
が3重に接している場合もこの証明の中で示せている.
(2) ![]() の場合.
の場合.
2直線![]() と
と![]() の交点を
の交点を![]() とする.
(1)の証明の後半と同様に,
とする.
(1)の証明の後半と同様に,
![]() で定まる対合に関して
で定まる対合に関して![]() は自己対合である.
一方,
2直線
は自己対合である.
一方,
2直線
![]() ,
,
![]() の積は曲線束
の積は曲線束![]() に属する分解した二次曲線である.
曲線束
に属する分解した二次曲線である.
曲線束![]() の直線
の直線![]() 上の対合に関して
2直線
上の対合に関して
2直線
![]() ,
,
![]() の積の自己対合点はその交点である.
よって
の積の自己対合点はその交点である.
よって![]() は2直線
は2直線
![]() ,
,
![]() の交点と一致する.
かくして2直線
の交点と一致する.
かくして2直線
![]() ,
,
![]() の積が
直線
の積が
直線![]() と1点を共有し,これが求める
と1点を共有し,これが求める![]() である.
である.
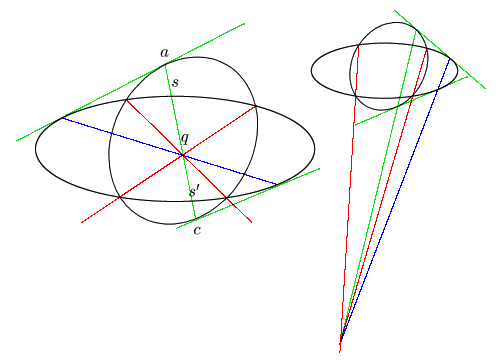
その他の点が一致する場合,つまり右図のようになるときもあるが, その場合の証明は同じである. □
実平面の円束に関する補題を確認しよう.
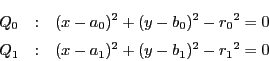
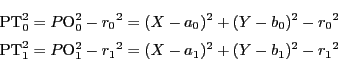
これから次のような別証明ができる.
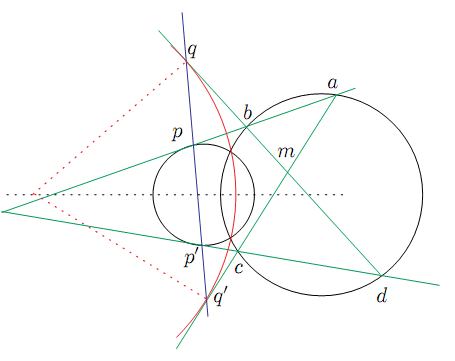 円周角の定理によって
円周角の定理によって
![]() ,
,
![]() である.
よって三角形
である.
よって三角形![]() と
と
![]() は相似であり
は相似であり
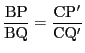 である.
同様にして
三角形
である.
同様にして
三角形![]() と
と![]() は相似であり
は相似であり
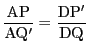 である.
である.
三角形の正弦定理から
直線![]() と
と![]() の交点を
の交点を![]() とすると,
三角形
とすると,
三角形![]() は二等辺三角形で
は二等辺三角形で
![]() となる.よって
2点
となる.よって
2点
![]() で
で
![]() に接する円
に接する円![]() が存在する.
が存在する.
![]() 上の4点
上の4点
![]() から
から![]() への
接線の長さの比はすべて等しく.円
への
接線の長さの比はすべて等しく.円![]() は
は![]() ,
,![]() と同じ円束に属する.いいかえれば
と同じ円束に属する.いいかえれば![]() は円
は円![]() は
は![]() で定まる円束の円である.
で定まる円束の円である.
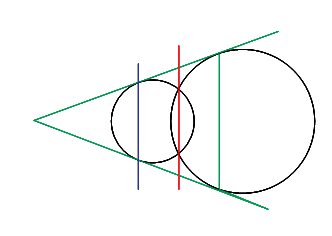
![]() の場合は
の場合は![]() と
と![]() の他の2共有点を結ぶ直線が平行となり,
2虚点を結ぶ無限遠直線
の他の2共有点を結ぶ直線が平行となり,
2虚点を結ぶ無限遠直線![]() の4直線が共点となることから示される.
□
の4直線が共点となることから示される.
□
このようにして円の場合に証明されたことを, 射影変換でもとに戻すことにより, 一定の条件を満たす任意の円錐曲線での命題が示される.
証明
![]() に対し,
に対し,
![]() と
と![]() がともに
がともに![]() に接するので,
定理97より
に接するので,
定理97より
![]() と
と
![]() が接する曲線束の円錐曲線と
が接する曲線束の円錐曲線と
![]() と
と
![]() が接する曲線束の円錐曲線が存在する.
が接する曲線束の円錐曲線が存在する.![]() に接する曲線束の要素は一意に定まるので,
これらの円錐曲線は同一である.これを
に接する曲線束の要素は一意に定まるので,
これらの円錐曲線は同一である.これを![]() とする.
とする.
![]() と
と
![]() がともに
がともに![]() に接するので,
再び定理97より直線
に接するので,
再び定理97より直線![]() が接する曲線束
が接する曲線束![]() の円錐曲線
の円錐曲線![]() が存在する.
□
が存在する.
□
![]() のとき成立するとする.
のとき成立するとする.
![]() が接する曲線束
が接する曲線束![]() に属する円錐曲線
に属する円錐曲線![]() が存在する.
一方
が存在する.
一方
![]() は
は![]() に接している.
命題98において,
に接している.
命題98において,![]() を
を
![]() とすることによって,
とすることによって,
![]() が接する
が接する![]() の要素が存在することが示された.
の要素が存在することが示された.
よって![]() に対してつねに成立する.
□
に対してつねに成立する.
□
このポンスレの定理を根拠として,閉形定理が示される.
定理 13 (閉形定理)
自然数![]() を
を![]() とする.
与えられた円錐曲線
とする.
与えられた円錐曲線![]() 上に頂点をもつ
上に頂点をもつ![]() 角形
角形
![]() で,
辺
で,
辺
![]() が
一つの円錐曲線
が
一つの円錐曲線![]() に接しているものが存在する.
このとき,
に接しているものが存在する.
このとき,![]() 上の任意の点
上の任意の点![]() をとり,順次
をとり,順次
![]() を
を
![]() が
が![]() に接するようにとる.
このとき残る辺
に接するようにとる.
このとき残る辺![]() も
も![]() に接する.
■
に接する.
■