次: 空間と変換群 上: 非ユークリッド幾何 前: 非ユークリッド幾何

第五公理の独立性

非ユークリッド幾何の発見

ユークリッド幾何学が広まるにつれ，多くの人が他の公理から平行線の公理を証明しようと試みた．公理5)は他と比べてずっと複雑だから，簡単な他の公理から導けるのではないか．多くの人がそのように考えたのだ．公理5)を否定して矛盾を導くという研究も容易に実を結ばなかった．

19世紀になると，公理5)を否定しても，矛盾のない論理体系としての幾何学が構成できるのではないか，と考えられるようになった．そしてついに1830年頃，ロバチェフスキー(ロシアの数学者，1793〜1856)とヤノス・ボーヤイ(現・ルーマニアの数学者，1802〜1860)によって独立にそのような幾何学が発見された．これらの幾何学はユークリッドのはじめの4つの公理はそのままとして，公理5)の代わりにその否定

5')

直線とその上にない点に対し， その点を通りその直線に平行な直線が2つ存在する．

5'')

直線とその上にない点に対し， その点を通りその直線に平行な直線が存在しない．

を公理として採用するというものであった．これはガウスにより非ユークリッド幾何学と名づけられた． 19世紀初頭から中期にかけてのことであった．その後19世紀末になって，非ユークリッド幾何の存在が，公理5)は他の公理から導くことはできないことを意味することが認識されていった．

それは，公理1)から公理4)までは成立するが，公理5)が成立しないようなモデルを構成すればよい．そのようなモデルが存在するということは，公理1)から公理4)を用いて公理5)を証明することはできないはずだ．

このような考え方は，はじめからあったのではない．ロバチェフスキーやボーヤイは非ユークリッド幾何学の体系そのものを考察の対象としたとはいえない．このような体系における公理5)の独立性などの問題意識は，集合論の矛盾などが発見され数学の基礎づけが大きな問題となったなかで，形成された．

このモデルを用いる論証は，クライン(F.Klein,1849〜1925)が，25才のときにはじめて指摘した．ロバチェフスキーの幾何学から30年目のことで，ちなみに後で紹介するヒルベルトの『幾何学基礎論』がはじめて世に出るのはここからさらに30年後のことだ．

2本の平行線

1点を通りある直線に平行な直線が2本存在する幾何のモデルはつぎのように構成される．これがはじめて見出された非ユークリッド幾何である．

例 5.2.1  定円の内部を空間とし，弦(両端は含まない)を直線とする． 円周とその外部は無限遠とする．円周上で交わる2直線は，平行である．

     このとき2点を通る直線がただ一つ存在する．また定点を通り直線$\mathrm{AB}$と平行な直線が2本引ける．

     定円の内部を空間とし，弦(両端は含まない)を直線とする．この弦$\mathrm{AB}$の円周上の端点を $\mathrm{P},\ \mathrm{Q}$とするとき，2点$\mathrm{AB}$の距離を

$$\log\dfrac{\mathrm{PB}}{\mathrm{PA}} \cdot\dfrac{\mathrm{BQ}}{\mathrm{AQ}}$$

で定める．

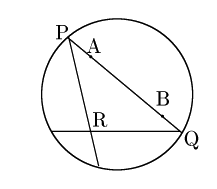
これは，複比にもとづく距離である． このモデルは公理1〜公理4を満たす．

そして，公理5)に代えて，公理5')が成り立つ．

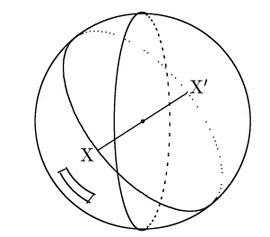平行線が存在しない

公理1)〜公理4)は満たすが，平行線が1本もないモデルを示す．

例 5.2.2   球面の表面上の点$\mathrm{X}$に対し，$\mathrm{X}$と球の中心に関して対称な位置にある点を$\mathrm{X}'$とする．$\mathrm{X}$と$\mathrm{X}'$を同一視し， $(\mathrm{X},\ \mathrm{X}')$の組を「点」とする．球面上の円で，円が乗っている平面が球の中心を通るものを大円と呼ぶが，大円を直線とする．2つの大円が交わる点での接線のなす角を2直線の角とする．

2点間の距離は，2点を結ぶ大円弧長とする．大円の周の$\dfrac{1}{2}$を法として定まる．

このときこのモデルは公理1)〜公理4)を満たす． しかしすべての直線は1点で交わるので，公理5)は満たさず，5'')が成立する．

1)

点として $\mathrm{X}$を用いようと$\mathrm{X}'$を用いようと， いずれかを通る大円は他方も通る．2点を通る大円は， 2点と球の中心を通る平面と球面の交わりの大円で， これはただ一つに定まる．

2)

同様に有限直線（線分）は， それが乗っている大円をただ一つ定める．

3)

任意の距離に対し大円の周の半分を法として， 大円の周の半分までの長さをとり，与えられた点との距離が この値となる点の集合をとればよい．

4)

任意の2点とそこを通る直線について， 一方の点を移動して他方の点にあわせ， さらに必要なら点の周りに直線を回転し， 他方の直線とあわせることができる．このとき， その点を通り二つのなす角が等しい直線は1本しかないので， すべての直角は相等しい．

このモデルでは，三角形の内角の和は$180^{\circ}$より大きい．ユークリッド幾何で，三角形の内角の和が$180^{\circ}$であることは，左図のように，平行線を引いて錯角の性質を用いて，3頂点の角を集めるとちょうど直線になることで示すのだった．

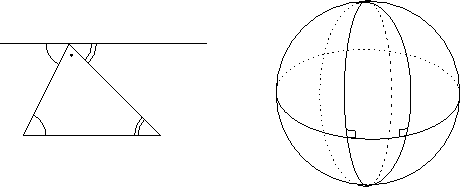
ところが右図のように，直交2直線が交わるのだから，三角形の内角の和は$180^{\circ}$より大きい．いずれにせよ，平面幾何で必要なことはこのモデルでもそろっている．しかし，平行線公理は成立しない．

だから，公理5)は他の公理からは導けない．導けるのなら，他の公理はすべて満たすこちらのモデルでも成立しなければならない．もし，公理1)〜公理4)から公理5)を導くことができるのなら，このようなモデルが存在することと矛盾する．

これらの例はすべて，ユークリッド幾何の平面の中に作られている．それによって，ユークリッド幾何が矛盾ない体系であるならば，これらの非ユークリッド幾何もまた矛盾がないことが示される．

ユークリッドの幾何は，普通の，われわれが住んでいる平面がモデルとなる幾何でもあるが，同じ頃，物理学の分野でアインシュタインによって相対性理論が発見され，展開された．相対性理論によって時間と空間を統一的に把握すると，それは最早ユークリッドの世界ではない．