次: 確率空間の積 上: 条件付確率 前: 条件付確率の定義

事象の独立

定義 2        確率空間$(U,\ p)$の2つの事象$A$と$B$に対して

$$p_A(B)=p(B)$$

が成り立つとき，事象$A$と$B$は互いに独立という．

言うまでもなく，この等式は

$$p(A\cap B)=p(A)p(B)$$

と同値である．

根元事象が同様に確からしく，集合の要素の個数で確率が決まるときは，図のように

$$\dfrac{n(A\cap B)}{n(A)}=\dfrac{n(B)}{n(U)}$$

となるということである．

確認問題 2       解答2

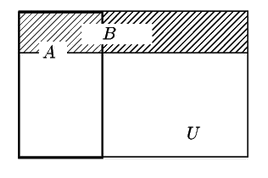
いずれの目が出る確率も同様に確かなサイコロがある． このサイコロの1の目から$m$の目までの面を赤く塗り， $m+1$の目から6の目までの面を青く塗る．ただし$1\le m \le 5$とする． このサイコロを投げるとき， 赤の面が出るという事象を$A$， 偶数の面が出るという事象を$B$とする． 事象$A$と事象$B$が独立となるような$m$の値を求めよ．

事象の独立と試行の独立

「試行の独立」，あるいは「独立試行」という用語は，教育現場に混乱をもたらしている．

ある教科書は「同じ状態のもとでくりかえすことができる」ことを試行の条件として書く． そのうえで「2つの試行が互いに他方の結果に影響しないとき，これらの試行は独立であ る」と書く．

そして，独立でない試行の例として，くじを1回目に引く試行をS，2回目に引く試行をTと したうえで，「引いたくじをもとに戻さない場合」をあげる．

しかしこの場合，1回目に当たりを引くか外れを引くかで，2回目にくじを引く条件が異な る．2回目のTは「同じ状態のもとでくりかえすことができる」という条件に反するので， 試行とは言えないのではないか． このような疑問が寄せられた．これは当然である．

また，この教科書は

     2つの独立な試行$S$，$T$を行うとき，$S$で$A$が起こり， $T$で$B$が起こる事象を$C$とすると，事象$C$の確率は

$$P(C)=P(A)P(B)$$

と書く．事象の独立は，積事象の確率が確率の積になることとして定義された． ところが，この記述では，何の論証もなしに，この等式が提示される． いったいこの等式は「2つの試行$S$，$T$が独立である」ことの定義なのか， あるいは結論として出てくるものなのか不明である．

ではどのように考えるべきなのか．

試行とは，手順「戻して$n$回引く」とか，「戻さずに$n$回引く」などの規則にもとづく一連の行為全体を意味し，それによって定まる確率空間を基礎とする，というのが確率論の立場である．

$n$回くじを引くとき，その結果は（◯××◯…）のような$n$個の◯と×の順列の全体である．戻すときも戻さないときも，その確率は計算できる．そのなかで1回目当たりという事象は(◯△△…)（△はどちらでもよい）の形をした部分集合であり，その確率も計算できる．2回目当たりという事象は(△◯△…)の形をした部分集合，1，2回目当たりという事象は(◯◯△…)の形をした部分集合である．その確率も計算できる．

これが任意の$k$回目と$l$回目で計算でき，その事象が独立か否かが定まる． $k$回目の事象と$l$回目の事象が，各$k$と$l$で独立なとき， その試行を「独立試行」という．それぞれの回の確率的行為が独立という意味ではない．$n$回くじを引くという試行の性質なのである．

実際，かつては教科書もそのようになっていた． 手元にある1969年の実教出版の教科書では，「独立試行」の「独立」はこの手順の性質としてつけられた形容詞であって，1回1回の確率的行為が独立という意味ではない．

このように，独立試行という概念は， 事象の独立のなかに含むことができ， またそうしてこそ，確率論の記述となる．