次: 確率変数の独立 上: 確率分布 前: 期待値の定義

和の期待値

確率変数$X$ が $x_1,\ x_2,\ \cdots,\ x_n$ の値を取り， その確率が $p_1,\ p_2,\ \cdots ,\ p_n$ であるとする． つまり $P(X=x_i)=p_i\ (i=1,\ 2,\ \cdots,\ n)$であるとする．

確率変数$Y$ は $y_1,\ y_2,\ \cdots ,\ y_m$ の値を取り， その確率が $q_1,\ q_2,\ \cdots ,\ q_m$ であるとする． つまり $P(Y=y_i)=q_i\ (i=1,\ 2,\ \cdots,\ m)$であるとする．

定理 3        確率変数$X+Y$の期待値 $E(X+Y)$ は $E(X)+E(Y)$ と一致する．

証明

$$\begin{eqnarray*} \sum_{i=1}^nP(X=x_i,\ Y=y_j)&=&P(Y=y_j)=q_j\\ \sum_{j=1}^mP(X=x_i,\ Y=y_j)&=&P(X=x_i)=p_i \end{eqnarray*}$$

なので

$$\begin{eqnarray*} E(X+Y)&=&\sum_{i=1}^n \sum_{j=1}^m (x_i+y_j)P(X=x_i,\ Y=y_j)\... ...)\\ &=&\sum_{i=1}^nx_ip_i+\sum_{j=1}^my_jq_j\\ &=&E(X)+E(Y) \end{eqnarray*}$$

である． □

注意 3        $P(X=x_i,\ Y=y_j)$は$X=x_i$かつ$Y=y_j$となる確率を表す．

注意 4        本定理は，$n$個の確率変数， $X_1,\ X_2,\ \cdots,\ X_n$に関する等式，

$$E\left(\sum_{k=1}^nX_k \right)= \sum_{k=1}^nE(X_k$$

に一般化される．証明は，数学的帰納法による．

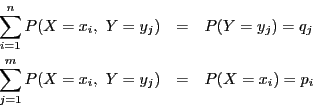
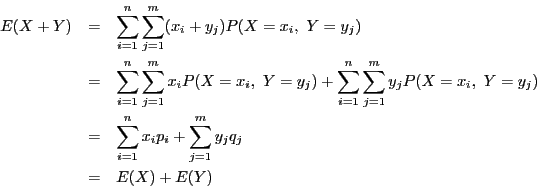
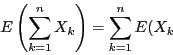
このような性質を，線形性という． 期待値は線形性をもつ．

期待値は根元事象の全体にわたる和であるという観点から $E(X+Y)=E(X)+E(Y)$を示すこともできる． $X$の値が$x_i$であり，$Y$の値が$y_j$であるような事象を$A_{i,j}$とおく．すると標本空間$U$は 互いに排反な事象$A_{i,j}$の和になる．そして

$$P(X=x_i,\ Y=y_j)=p(A_{ij})=\sum_{u \in A_{i,j}}p(u)$$

である．$u\in A_{ij}$に対して

$$x_i+y_j=X(u)+Y(u)$$

なので

$$\begin{eqnarray*} (x_i+y_j)P(X=x_i,\ Y=y_j)&=&(x_i+y_j)\left\{\sum_{u \in A_{i,... ...\right\}\\ &=&\sum_{u \in A_{i,j}}\left(X(u)+Y(u) \right)p(u) \end{eqnarray*}$$

したがって

$$\begin{eqnarray*} E(X+Y)&=&\sum_{i=1}^n \sum_{j=1}^m (x_i+y_j)P(X=x_i,\ Y=y_j)\... ...\\ &=&\sum_{u \in U}X(u)p(u)+\sum_{u \in U}Y(u)p(u)=E(X)+E(Y) \end{eqnarray*}$$

確認問題 4       解答4

10円硬貨3枚，50円硬貨5枚を同時に投げる．確率変数$X$を表の出た硬貨の 金額の和とする．$X$の期待値を求めよ．

問題 5       ［04北大前期理系］    解答5

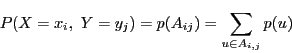
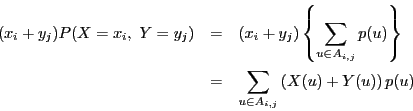
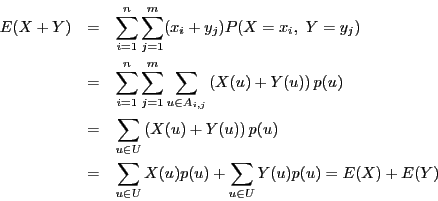
ある人がサイコロを振る試行によって，部屋A，Bを移動する. サイコロの目の数が1，3のときに限り部屋を移る． また各試行の結果，部屋Aに居る場合はその人の持ち点に1点を加え，部屋Bに居る場合は1点を減らす． 持ち点は負になることもあるとする． 第$n$試行の結果，部屋A，Bに居る確率をそれぞれ $P_A(n),\ P_B(n)$と表す． 最初にその人は部屋Aに居るものとし(つまり， $P_A(0)=1,\ P_B(0)=0$とする)，持ち点は1とする．

1. $P_A(1),\ P_A(2),\ P_A(3)$および $P_B(1),\ P_B(2),\ P_B(3)$を求めよ． また，第3試行の結果，その人が得る持ち点の期待値$E(3)$を求めよ．
2. $P_A(n+1),\ P_B(n+1)$を $P_A(n),\ P_B(n)$を用いて表せ．
3. $P_A(n),\ P_B(n)$を$n$を用いて表せ．
4. 第$n$試行の結果，その人が得る持ち点の期待値$E(n)$を求めよ．

分散と標準偏差

ある確率変数$X$に対し，その期待値を$E(X)$とする． 期待値は同じでも，確率変数の値が大きく変化しているときや， 期待値の近くにかたまっている場合など，散らばり具合はいろいろある． それを数値化するために，

$$V(X)=E((X-E(X))^2)$$

とおく．$(X-E(X))^2$は新たな確率変数であり，その期待値が$V(X)$である． この値を分散という． 各確率変数の値が期待値からどれだけ離れているかは $\vert X-E(X)\vert$である．その平方の期待値が分散である．

$V(X)$は期待値の線形性を用いて簡単にすることができる．

$$\begin{eqnarray*} V(X)&=&E((X-E(X))^2)\\ &=&E(X^2-2E(X)X+ E(X))^2)\\ &=&E(X... ...(E(X)^2)\\ &=&E(X^2)-2(E(X))^2+ E(X)^2\\ &=&E(X^2)-(E(X))^2 \end{eqnarray*}$$

この式は分散の意味は見えにくいが，計算はこちらが便利である．

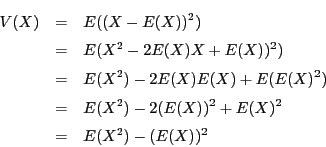
そして，平方の期待値の平方根，つまり

$$\sigma(X)=\sqrt{V(X)}$$

を標準偏差という．