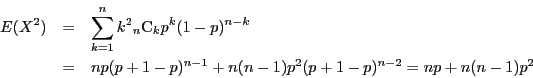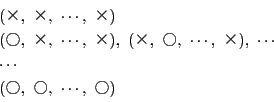
このような試行を反復試行という.
標本空間は
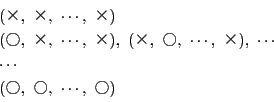
このとき,![]() 回中にそのことが起こる回数という確率変数を
回中にそのことが起こる回数という確率変数を![]() とする.
この確率変数は,
とする.
この確率変数は,![]() の範囲の整数
の範囲の整数![]() に対して
に対して
実際,その独立性により,![]() 回起こる各々の確率が
回起こる各々の確率が![]() で,
それが
で,
それが
![]() 通りあるから,
通りあるから,
![]() となる確率は
となる確率は
![]() である.
である.
この確率分布は,二項定理
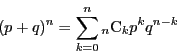
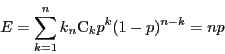
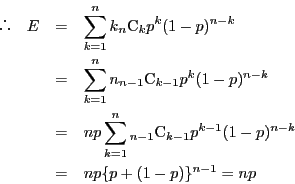
このように,反復試行の確率は,二項分布という分布を与えるモデルとしてとらえたとき, はじめてその発展的な意味がつかめる. ここで,二項分布に係わる問題を紹介しよう.
2枚の硬貨があり,1枚ずつ投げたとき表の出る確率をそれぞれ ![]() ,
,![]() とする.
2枚同時に投げたとき,表の出た硬貨の枚数を
とする.
2枚同時に投げたとき,表の出た硬貨の枚数を ![]() とする.
従って,確率変数
とする.
従って,確率変数 ![]() は値 0,1,2 をとり,その確率分布は
は値 0,1,2 をとり,その確率分布は ![]() ,
,![]() により定まる.
逆に
により定まる.
逆に ![]() の分布を指定したとき,その分布を与えるような
の分布を指定したとき,その分布を与えるような ![]() ,
,![]() の値が存在するかどうか,
また存在する場合には,どれだけあるか,次の2つの場合について答えよ.
の値が存在するかどうか,
また存在する場合には,どれだけあるか,次の2つの場合について答えよ.
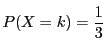 (
(
![]() を3以上の自然数とする.スイッチを入れると等確率で赤色または青色に輝く電球が横一列に
を3以上の自然数とする.スイッチを入れると等確率で赤色または青色に輝く電球が横一列に![]() 個並んでいる.
これらの
個並んでいる.
これらの![]() 個の電球のスイッチを同時に入れたあと,左から電球の色を見ていき,色の変化の回数を調べる.
個の電球のスイッチを同時に入れたあと,左から電球の色を見ていき,色の変化の回数を調べる.
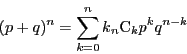
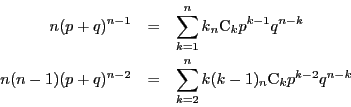
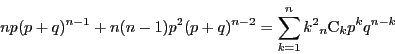
二項分布![]() の期待値
の期待値![]() は,先に見たように
は,先に見たように