これを少し一般化しよう.
2つの確率空間![]() と
と![]() があり,
があり,
![]() と
と![]() はそれぞれ
はそれぞれ![]() と
と![]() の事象だけで定まり,
たがいに
の事象だけで定まり,
たがいに![]() と
と![]() の事象とは無関係であるとする.
つまり,
の事象とは無関係であるとする.
つまり,![]() の
の![]() が起こったとき,
が起こったとき,
![]() ではその何れもが,
ではその何れもが,![]() で定まる確率で起こりうる,
で定まる確率で起こりうる,
![]() ,
,![]() でも同様ということである.
でも同様ということである.
![]() と
と![]() はそれぞれ
はそれぞれ![]() と
と![]() の事象だけで定まり,
たがいに
の事象だけで定まり,
たがいに![]() と
と![]() の事象とは無関係であるとの仮定が,
埋め込みができることと同値である.
の事象とは無関係であるとの仮定が,
埋め込みができることと同値である.
証明
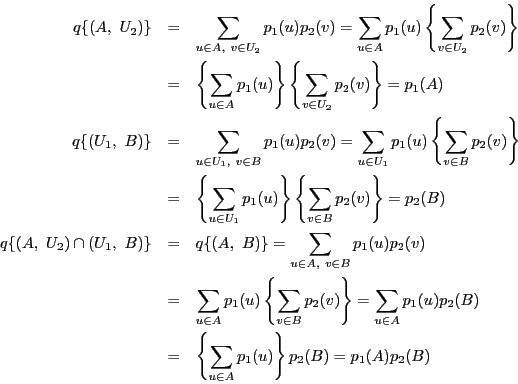
これによって
![]() の根元事象の確率が相等しく,
の根元事象の確率が相等しく,![]() の根元事象の確率も相等しく,
かつ,2つの標本空間
の根元事象の確率も相等しく,
かつ,2つの標本空間![]() と
と![]() の積集合に,事象
の積集合に,事象![]() や
や![]() が
が![]() ,
,![]() の形で埋め込めることができるとする.
の形で埋め込めることができるとする.
それぞれの事象の![]() ,
,![]() での確率は,
での確率は,
![]() ,
,
![]() である.
そして,
である.
そして,
よって標本空間![]() での事象
での事象![]() の確率は
の確率は
逆にいうと,先の![]() の確率
の確率![]() の定義は自然なものである.
の定義は自然なものである.
標本空間2個の積は,![]() 個の積にそのまま一般化される.
個の積にそのまま一般化される.