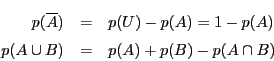
が成り立つ.
これらは,集合の記号をそのまま用いている.
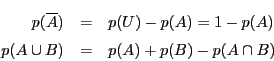
証明
![]() で
で
![]() なので確率の定義(3)から
なので確率の定義(3)から
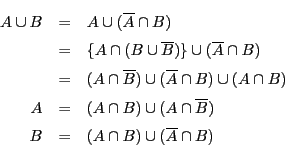
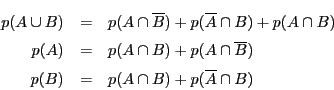
さらに教科書は,この公式から
![]() のとき,事象
のとき,事象![]() と事象
と事象![]() は互いに排反であるという.
確率の公理から
は互いに排反であるという.
確率の公理から
確率を全ての事象に確率値を対応させる関数として定義した. 事象はすべて根元事象の和集合になるので,根元事象の確率が定まっていれば, 一般の事象の確率はそれを構成する根元事象の確率の和になるのではないか.
根元事象が有限個の場合はその通りなのだ.また
無限個あっても
![]() と数えられるような可算無限の場合も含めて,
事象
と数えられるような可算無限の場合も含めて,
事象![]() の確率
の確率![]() は
は
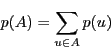
ところが連続的な確率の場合にはこれでは定義にならない. これについては,最後の「連続的確率」を参照してほしい.
以下,「無限標本空間」までは標本空間が有限集合であるものとする.