

 次: 一次不定方程式の一般解と解の構成
上: 一次不定方程式
前: 不定方程式
次: 一次不定方程式の一般解と解の構成
上: 一次不定方程式
前: 不定方程式
定理 4

と

は互いに素な整数である.このとき,
一次不定方程式
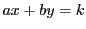
には整数解が存在する.
■
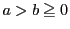 のとき解をもつことが示せれば,例えば
のとき解をもつことが示せれば,例えば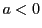 なら
なら
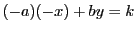 を考えればこの場合も整数解があることがわかる.
よって
を考えればこの場合も整数解があることがわかる.
よって と
と は
は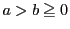 である互いに素な整数とする.
である互いに素な整数とする.
この定理には三通りの証明法がある.それを実行し比較検討しよう.
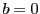 のとき,
のとき, 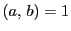 より
より 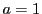 .ゆえに方程式は
.ゆえに方程式は
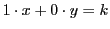 となるから,解
となるから,解 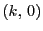 をもつ.
をもつ.
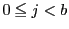 の
の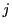 と
と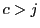 で
で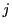 と互いに素な任意の
と互いに素な任意の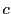 に対して
に対して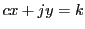 が解をもつとする.
このとき
が解をもつとする.
このとき
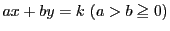 が解をもつことを示す.
が解をもつことを示す.
とする.このとき,
 と
と  が互いに素なので
が互いに素なので  と
と  も互いに素である.
ゆえに,仮定より
も互いに素である.
ゆえに,仮定より 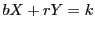 は解
は解 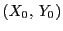 をもつ.この解に対して
をもつ.この解に対して
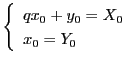 を解くと
を解くと
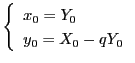 となる.
となる.
この 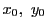 は
は
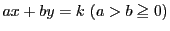 の解となっている.実際
の解となっている.実際
つまり, のときも成立する.
のときも成立する.
よって, 数学的帰納法により, すべての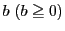 と,
と,
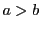 なる
なる  に対し
に対し 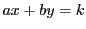 は解をもつ. □
は解をもつ. □
有限個のもののなかに,
ある条件を満たすものが存在することを示す根拠としてよく用いられるのが
鳩の巣原理とか部屋割り論法とかいわれる次の原理である.
同等な二つの形が用いられる.
- (i)
 人を
人を 部屋に分ける.
部屋に分ける.
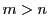 なら,2人以上入る部屋が存在する.
なら,2人以上入る部屋が存在する.
- (ii)
 人を
人を 部屋に分ける.
相部屋になる者がないなら,すべての部屋に入る.
部屋に分ける.
相部屋になる者がないなら,すべての部屋に入る.
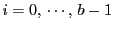 に対して
に対して 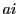 を
を  で割った余りを
で割った余りを 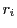 とする.
各
とする.
各 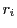 は0から
は0から 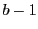 のどれかの値をとる.
のどれかの値をとる.
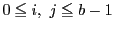 に対して
に対して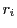 と
と 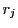 が
が 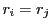 とする.
とする.
より
 と
と  が互いに素なので
が互いに素なので 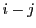 が
が  の倍数である.
の倍数である.
より,この範囲の の倍数は,
の倍数は,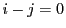 以外にない.
対偶をとると,
以外にない.
対偶をとると,
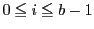 の
の 個の
個の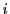 に対して,
同じ範囲の値
に対して,
同じ範囲の値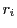 が対応し,これらのうちに同じ値がない.
鳩の巣原理によって
が対応し,これらのうちに同じ値がない.
鳩の巣原理によって
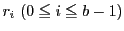 は0から
は0から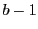 の各値を一つずつとる.
の各値を一つずつとる.
 を
を で割って商が
で割って商が ,余りが
,余りが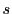 とする.
とする.
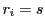 となる
となる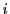 が存在する.
つまり
が存在する.
つまり
となる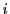 と
と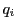 が存在する.
が存在する.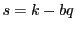 なので
なので
つまり
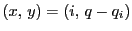 が
が 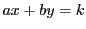 の解である.
□
の解である.
□
注意 1.4.1
これは解の作り方も教えている.例えば
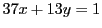
の一組の解を見つけるためには次のようにすればよい.
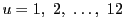 に対して
に対して 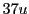 を
を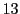 で割った余りを書いていく.
で割った余りを書いていく.
かならず1が出てくる.実際
ゆえに
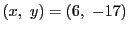
が解である.
整数からなる集合 を
を
で定める. の要素で正のものからなる集合は自然数の部分集合なので, そのなかに最小のものが存在する.それを
の要素で正のものからなる集合は自然数の部分集合なので, そのなかに最小のものが存在する.それを とし,
とし,
とする.
 の任意の要素
の任意の要素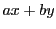 を
を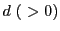 で割る.
で割る.
である.これから
なので, も
も の要素である.
の要素である.
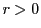 なら
なら が
が の要素のなかで正で最小のものであることに矛盾する.
よって
の要素のなかで正で最小のものであることに矛盾する.
よって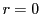 である.
である.
 の任意の要素は
の任意の要素は の倍数であることが示された.
逆に
の倍数であることが示された.
逆に の倍数
の倍数
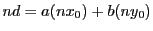 は
は の要素である.
の要素である.
次に
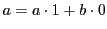 なので
なので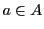 ,同じく
,同じく 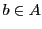 も成立する.
よって
も成立する.
よって と
と は
は の倍数,つまり
の倍数,つまり  は
は  と
と  の公約数である.
ところが
の公約数である.
ところが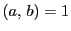 なので,
なので,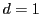 である.
である.
ゆえに は整数の集合と一致する.したがって任意の整数
は整数の集合と一致する.したがって任意の整数 に対して
方程式
に対して
方程式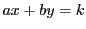 には解が存在する. □
には解が存在する. □
この三つの証明のなかで,未知数が3個以上ある場合に拡張しうるのはどれか.
数学的帰納法は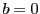 のとき未知数がひとつ減るだけでしかない.
したがって未知数に関する帰納法と
のとき未知数がひとつ減るだけでしかない.
したがって未知数に関する帰納法と  に関する数学的帰納法を組み合わせなければならない.
不可能ではないが,もっと簡明にできないか.
第二の証明も未知数の個数に関する数学的帰納法が必要になる.
第三の証明はどうだろうか.これは明らかに一般の場合にそのまま拡張される.
に関する数学的帰納法を組み合わせなければならない.
不可能ではないが,もっと簡明にできないか.
第二の証明も未知数の個数に関する数学的帰納法が必要になる.
第三の証明はどうだろうか.これは明らかに一般の場合にそのまま拡張される.
ここでは第三の場合の証明のなかで用いられた方法を取りだして補題とし,
それを用いて一般の場合を証明しよう.
補題 1
整数からなる集合

は次の性質を持つ.
このとき

は

に属する正で最小の要素の倍数全体からなる集合である.
■
証明
条件から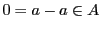 である.
また
である.
また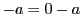 から
から 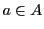 なら
なら 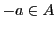 である.したがって
である.したがって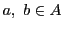 に対して
に対して
である.
 の任意の要素
の任意の要素  と整数
と整数  に対して
に対して 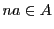 であることを数学的帰納法で示す.
であることを数学的帰納法で示す.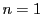 なら明らか.
なら明らか. 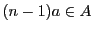 と仮定すれば
と仮定すれば
である.よって示された.
さて,集合  に含まれる正で最小の要素を
に含まれる正で最小の要素を  とする.
とする.
 の任意の要素
の任意の要素  を
を  で割ったとき商が
で割ったとき商が  ,余りが
,余りが  であるとする.
であるとする.
すると上に示したことから 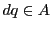 である.よって
である.よって
ここでもし 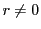 なら
なら  より小さい正数
より小さい正数  が
が  に属することになり
に属することになり  の最小性に反する.
の最小性に反する.
つまり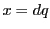 となり,
となり, の任意の要素は
の任意の要素は  の倍数であることが示された.
の倍数であることが示された. の倍数が
の倍数が に属することはすでに示されている.□
に属することはすでに示されている.□
定理 5 (一次不定方程式の解の存在定理)
整数
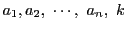
を係数とする一次不定方程式
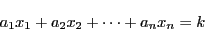 |
(1.2) |
が解をもつための必要十分条件は,
整数

が整数
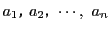
の最大公約数
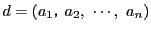
で割り切れることである.■
証明
集合
を考える.
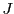 の任意の2つの要素の差が再び
の任意の2つの要素の差が再び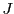 に属することは明らかである.
したがって
に属することは明らかである.
したがって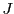 は
は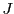 に含まれる正で最小の整数
に含まれる正で最小の整数 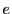 の倍数全体からなる集合である.
の倍数全体からなる集合である.
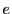 は
は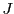 の要素なので
の要素なので
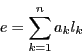 |
(1.3) |
となる
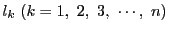 がある.
したがって
がある.
したがって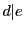 である.
である.
一方
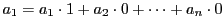 などから
などから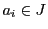 が各
が各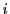 について成り立つ.
それらが
について成り立つ.
それらが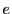 の倍数なので,
の倍数なので,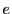 は
は
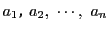 の公約数である.
つまり
の公約数である.
つまり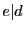 である.
である.
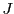 が
が の倍数全体の集合であることが確定したので,
方程式(1.2)が解をもつことと,
の倍数全体の集合であることが確定したので,
方程式(1.2)が解をもつことと, が
が の倍数であることの同値性が示された.
□
の倍数であることの同値性が示された.
□


 次: 一次不定方程式の一般解と解の構成
上: 一次不定方程式
前: 不定方程式
Aozora Gakuen
次: 一次不定方程式の一般解と解の構成
上: 一次不定方程式
前: 不定方程式
Aozora Gakuen
![]() のとき解をもつことが示せれば,例えば
のとき解をもつことが示せれば,例えば![]() なら
なら
![]() を考えればこの場合も整数解があることがわかる.
よって
を考えればこの場合も整数解があることがわかる.
よって![]() と
と![]() は
は![]() である互いに素な整数とする.
である互いに素な整数とする.
![]() の
の![]() と
と![]() で
で![]() と互いに素な任意の
と互いに素な任意の![]() に対して
に対して![]() が解をもつとする.
このとき
が解をもつとする.
このとき
![]() が解をもつことを示す.
が解をもつことを示す.
![]() と
と ![]() が互いに素なので
が互いに素なので ![]() と
と ![]() も互いに素である.
ゆえに,仮定より
も互いに素である.
ゆえに,仮定より ![]() は解
は解 ![]() をもつ.この解に対して
をもつ.この解に対して
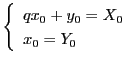 を解くと
を解くと
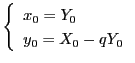 となる.
となる.
![]() は
は
![]() の解となっている.実際
の解となっている.実際
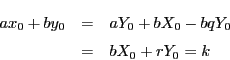
![]() と,
と,
![]() なる
なる ![]() に対し
に対し ![]() は解をもつ. □
は解をもつ. □
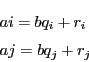
![]() を
を![]() で割って商が
で割って商が![]() ,余りが
,余りが![]() とする.
とする.
![]() となる
となる![]() が存在する.
つまり
が存在する.
つまり
![]() に対して
に対して ![]() を
を![]() で割った余りを書いていく.
で割った余りを書いていく.
![]() の任意の要素は
の任意の要素は![]() の倍数であることが示された.
逆に
の倍数であることが示された.
逆に![]() の倍数
の倍数
![]() は
は![]() の要素である.
の要素である.
![]() なので
なので![]() ,同じく
,同じく ![]() も成立する.
よって
も成立する.
よって![]() と
と![]() は
は![]() の倍数,つまり
の倍数,つまり ![]() は
は ![]() と
と ![]() の公約数である.
ところが
の公約数である.
ところが![]() なので,
なので,![]() である.
である.
![]() は整数の集合と一致する.したがって任意の整数
は整数の集合と一致する.したがって任意の整数![]() に対して
方程式
に対して
方程式![]() には解が存在する. □
には解が存在する. □
![]() のとき未知数がひとつ減るだけでしかない.
したがって未知数に関する帰納法と
のとき未知数がひとつ減るだけでしかない.
したがって未知数に関する帰納法と ![]() に関する数学的帰納法を組み合わせなければならない.
不可能ではないが,もっと簡明にできないか.
第二の証明も未知数の個数に関する数学的帰納法が必要になる.
第三の証明はどうだろうか.これは明らかに一般の場合にそのまま拡張される.
に関する数学的帰納法を組み合わせなければならない.
不可能ではないが,もっと簡明にできないか.
第二の証明も未知数の個数に関する数学的帰納法が必要になる.
第三の証明はどうだろうか.これは明らかに一般の場合にそのまま拡張される.
![]() である.
また
である.
また![]() から
から ![]() なら
なら ![]() である.したがって
である.したがって![]() に対して
に対して
![]() の任意の要素
の任意の要素 ![]() と整数
と整数 ![]() に対して
に対して ![]() であることを数学的帰納法で示す.
であることを数学的帰納法で示す.![]() なら明らか.
なら明らか. ![]() と仮定すれば
と仮定すれば
![]() に含まれる正で最小の要素を
に含まれる正で最小の要素を ![]() とする.
とする.
![]() の任意の要素
の任意の要素 ![]() を
を ![]() で割ったとき商が
で割ったとき商が ![]() ,余りが
,余りが ![]() であるとする.
であるとする.
![]() は
は![]() の要素なので
の要素なので
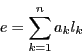
![]() などから
などから![]() が各
が各![]() について成り立つ.
それらが
について成り立つ.
それらが![]() の倍数なので,
の倍数なので,![]() は
は
![]() の公約数である.
つまり
の公約数である.
つまり![]() である.
である.