

 次: 素数
上: 一次不定方程式
前: 一次不定方程式の解の存在
次: 素数
上: 一次不定方程式
前: 一次不定方程式の解の存在
一次不定方程式
の一般解と解を構成するアルゴリズムの存在について考える.
まず「一般解」を正確に定義しておこう.二変数の場合についてのべる.
 と
と 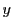 との不定方程式
との不定方程式 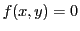 がある.
関数
がある.
関数 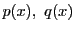 が存在し,この不定方程式の任意の解を
が存在し,この不定方程式の任意の解を
と表す整数 が存在し,
逆に任意の整数
が存在し,
逆に任意の整数 に対して
に対して
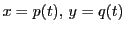 がこの不定方程式の整数解となるとき,
がこの不定方程式の整数解となるとき,
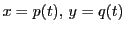 を不定方程式
を不定方程式 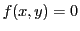 の一般解 という.
の一般解 という.
変数が多い場合も同様に定義される.
ただし二変数の場合は任意整数を表す変数の個数は1個であったが,
一般には変数
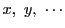 の個数から1減じた個数の任意整数が必要である.
の個数から1減じた個数の任意整数が必要である.
例 1.4.1
の一般解を求める.
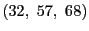
の最大公約数を求めるときと同様に,
いちばん小さい32で他の二数を割る.
これを係数に代入し同様の操作を繰り返す.
ここで
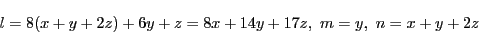 |
(1.4) |
とおく.
の一般解を求める.これは例えば.
がとれる.これより(
1.4)は
となる.これから一般解は
となる.
今は,適宜(てきぎ)式を整理したのでわかりにくいが,
この方法をまねて一般解を構成するアルゴリズムを定式化することができる.
上の例からわかることは,
除法をおこなうことで少ない変数の場合に帰着させ,
二変数の一般解を用いて一般解を構成できるのではないか,ということである.
そのためにまず二変数の場合について,確認しなければならない.
まず一組の解を見いださなければならない.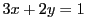 なら暗算でできる.
しかし
なら暗算でできる.
しかし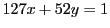 となると,一組見つけるのも暗算というわけにはいかない.
ところが,ユークリッドの互除法を用いて一組の解を構成する一般的な方法がある.
となると,一組見つけるのも暗算というわけにはいかない.
ところが,ユークリッドの互除法を用いて一組の解を構成する一般的な方法がある.
 と
と  の最大公約数が1より大きいとき,
の最大公約数が1より大きいとき,
 が,
が, と
と の最大公約数の倍数でなければ解はない.
の最大公約数の倍数でなければ解はない.
 が最大公約数の倍数なら全体をその最大公約数で割って,
初めから
が最大公約数の倍数なら全体をその最大公約数で割って,
初めから  と
と  の最大公約数は1,つまり
の最大公約数は1,つまり  と
と  は互いに素であるとしてよい.
このとき
は互いに素であるとしてよい.
このとき 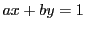 に解が見つかれば
に解が見つかれば  と
と 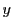 の各々に
の各々に  を乗じることにより,
を乗じることにより,
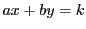 の解ができる.
結局
の解ができる.
結局  と
と  が互いに素なときに
が互いに素なときに 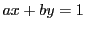 の解が構成できれば
よいことがわかる.
の解が構成できれば
よいことがわかる.
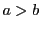 とし,
とし,
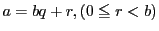 とする.
とする.
-
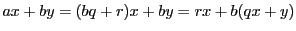 であるから,
であるから,
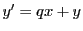 とおくと方程式
とおくと方程式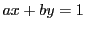 は方程式
は方程式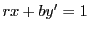 となる.
となる.
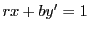 の解
の解 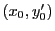 が構成できれば,
が構成できれば,
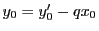 によって定めた
によって定めた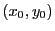 が
が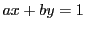 の解となる.
の解となる.
これは解の存在証明の第一の方法と同じ内容であることに注意しよう.
 と
と  が互いに素なら
が互いに素なら  と
と  も互いに素であるから,こうして係数のより小さい方程式が得られ,しかもその解からもとの方程式の解が構成できる.この過程を繰り返すと,最後は係数の一方は
も互いに素であるから,こうして係数のより小さい方程式が得られ,しかもその解からもとの方程式の解が構成できる.この過程を繰り返すと,最後は係数の一方は 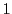 となる.
となる.
 または
または 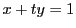 の解として
の解として
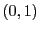 か
か 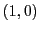 をとれる.
ここから逆に戻っていけば
をとれる.
ここから逆に戻っていけば 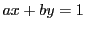 の解が得られる.
の解が得られる.
この方法で 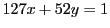 の解を構成しよう.
まず互除法で方程式を変換する.
の解を構成しよう.
まず互除法で方程式を変換する.
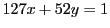
-
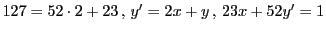
-
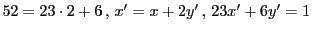
-
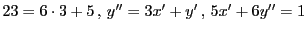
-
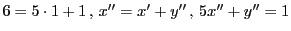
ここから逆に解を構成していく.
-
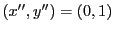
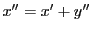 より
より
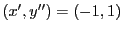
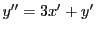 より
より
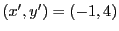
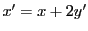 より
より 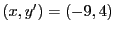
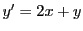 より
より 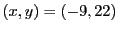
確かに,
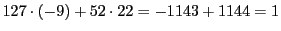 である.
これは二変数の不定方程式の解を構成する一般的な方法である.
である.
これは二変数の不定方程式の解を構成する一般的な方法である.
この過程を具体的に記述するのは二次行列を使うのが適切である.
二次行列の演算と行列式についてまとめておこう.
行列
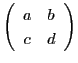 とベクトル
とベクトル
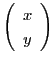 に対し,
に対し,
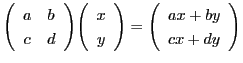 と定める.
と定める.
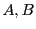 を二つの行列とし,
を二つの行列とし,
 とする.
このとき計算によって確認できるように,
とする.
このとき計算によって確認できるように,
が成り立つ.
また,行列
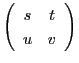 に対して,
に対して,
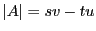 とおくと,
とおくと,
が成り立つ.
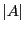 のことを行列
のことを行列  の「行列式」という.
の「行列式」という.
以上を前提に,二変数一次不定方程式の一般解の構成を含めて定理にまとめる.
定理 6
- (1)
-
 とする.
とする. を
を で割った商を
で割った商を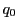 ,余りを
,余りを 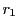 とするとき,
次式が成り立つ.
とするとき,
次式が成り立つ.
- (2)
- 同様の操作を繰り返すことにより,除法の列
に対して,
が得られる.ここで
と置く.このとき次式が成り立つ.
- (3)
 と
と  の最大公約数を
の最大公約数を  とするとき,
とするとき,
となる番号  が存在する.
が存在する.
- (4)
- このとき,
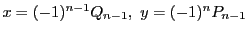 が不定方程式
が不定方程式
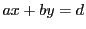 の一組の解となる.
の一組の解となる.
- (5)
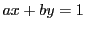 の1組の解があるとし,それを
の1組の解があるとし,それを
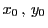 とする.
このとき
とする.
このとき 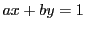 の一般解は,
の一般解は,
である.■
証明
(1)
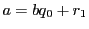 である. よって,
である. よって,
(2)
よって,
である.
(3)
 を
を  で割った除法の式を
で割った除法の式を
とする. この式の形より,  と
と  の公約数は
の公約数は 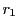 を割り,
を割り,  と
と 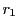 の公約数は
の公約数は
 を割るので,
を割るので,  と
と  の最大公約数と
の最大公約数と  と
と 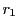 の最大公約数は等しい(ユークリッドの互除法の原理).
の最大公約数は等しい(ユークリッドの互除法の原理).
次に, 除法の原理より,
である. 同様に
はそれぞれの組の最大公約数がつねに等しく, かつ
と減少してゆく列である.ゆえに, ある番号  が存在して,
が存在して,
となる. このとき,  と
と  の最大公約数が
の最大公約数が 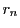 と
と 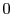 の最大公約数
( 0は0でない任意の整数を約数にもつものとする)となるので,
の最大公約数
( 0は0でない任意の整数を約数にもつものとする)となるので, 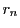 そのものが
そのものが と
と
 の最大公約数
の最大公約数  である. つまり, この
である. つまり, この  に対して,
に対して,
となる.
(4)
の両辺に
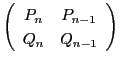 の逆行列を左からかけると,
の逆行列を左からかけると,
であるから,
つまり,
よって,
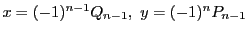 は
は 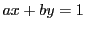 の解である.
の解である.
(5)
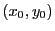 を
を 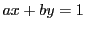 の任意の解の組とすると,
の任意の解の組とすると,
これより,
となり,  と
と  は互いに素であるから,
は互いに素であるから, 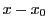 は
は  の倍数である.
よって,
の倍数である.
よって,
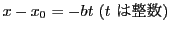 とおくと,
とおくと, 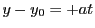 となる. つまり,
このときある
となる. つまり,
このときある  に対し,
に対し,
となる. 逆に, 任意の整数  に対し,
に対し,
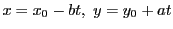 とおくと,
とおくと,
となるので, 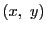 は
は 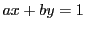 の解である. □
の解である. □
例 1.4.2
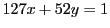
の一般解を以上の方法で求めよう.
そして,
なので,
が1組の解である. 実際,
よって, 一般解は任意の整数

に対し, 次式で与えられる.
このように二変数の場合について構成法が確立した.
これをもとに一般の  変数の場合に,帰納的に解を構成していくことができる.
変数の場合に,帰納的に解を構成していくことができる.
- (1)
- 二変数の場合,ユークリッドの互除法によって個別解が求まり,
それを用いて一般解を作ることができる.
- (2)
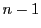 変数のとき一般解を構成することができるとする.
変数のとき一般解を構成することができるとする.
- (3)
-
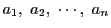 で
で 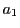 が絶対値最小とする.
が絶対値最小とする.
とする.はじめの方程式は
となる.ここで
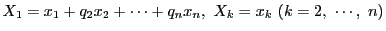 とおく.
とおく.
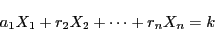 |
(1.5) |
ここで(1.5)の解
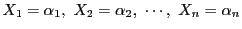 が構成できたとする.
このとき
が構成できたとする.
このとき
であるから
は
の解である.
よって(1.5)の解が構成できればよい.
ところが,方程式(1.5)を作った操作を繰り返すと,
ついにはいずれかの係数が0になる.
その0のものを除いた 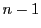 変数の不定方程式は一般解が構成できる.
係数 0 の未知数を新たな任意整数におく.
こうして得られた一般解から上の手順でもとの方程式の解を構成していけば,
必ずもとの不定方程式の解が構成される.□
変数の不定方程式は一般解が構成できる.
係数 0 の未知数を新たな任意整数におく.
こうして得られた一般解から上の手順でもとの方程式の解を構成していけば,
必ずもとの不定方程式の解が構成される.□
一般的な構成アルゴリズムの存在は,解の存在証明の別解になっていることに注意しよう.


 次: 素数
上: 一次不定方程式
前: 一次不定方程式の解の存在
Aozora Gakuen
次: 素数
上: 一次不定方程式
前: 一次不定方程式の解の存在
Aozora Gakuen
![]() と
と ![]() との不定方程式
との不定方程式 ![]() がある.
関数
がある.
関数 ![]() が存在し,この不定方程式の任意の解を
が存在し,この不定方程式の任意の解を
![]() の個数から1減じた個数の任意整数が必要である.
の個数から1減じた個数の任意整数が必要である.
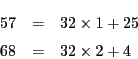
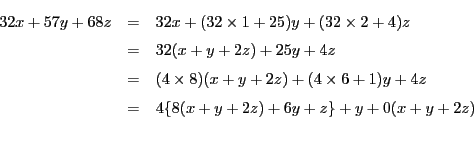
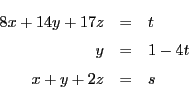
![]() と
と ![]() の最大公約数が1より大きいとき,
の最大公約数が1より大きいとき,
![]() が,
が,![]() と
と![]() の最大公約数の倍数でなければ解はない.
の最大公約数の倍数でなければ解はない.
![]() が最大公約数の倍数なら全体をその最大公約数で割って,
初めから
が最大公約数の倍数なら全体をその最大公約数で割って,
初めから ![]() と
と ![]() の最大公約数は1,つまり
の最大公約数は1,つまり ![]() と
と ![]() は互いに素であるとしてよい.
このとき
は互いに素であるとしてよい.
このとき ![]() に解が見つかれば
に解が見つかれば ![]() と
と ![]() の各々に
の各々に ![]() を乗じることにより,
を乗じることにより,
![]() の解ができる.
結局
の解ができる.
結局 ![]() と
と ![]() が互いに素なときに
が互いに素なときに ![]() の解が構成できれば
よいことがわかる.
の解が構成できれば
よいことがわかる.
![]() または
または ![]() の解として
の解として
![]() か
か ![]() をとれる.
ここから逆に戻っていけば
をとれる.
ここから逆に戻っていけば ![]() の解が得られる.
の解が得られる.
![]() の解を構成しよう.
まず互除法で方程式を変換する.
の解を構成しよう.
まず互除法で方程式を変換する.
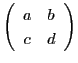 とベクトル
とベクトル
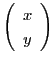 に対し,
に対し,
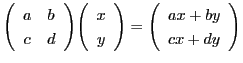 と定める.
と定める.
![]() を二つの行列とし,
を二つの行列とし,
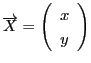 とする.
このとき計算によって確認できるように,
とする.
このとき計算によって確認できるように,
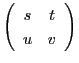 に対して,
に対して,
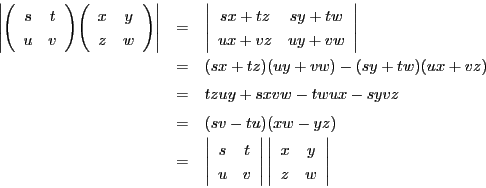
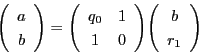
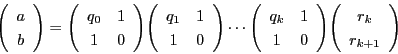
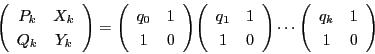
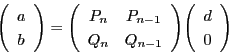
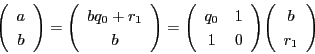
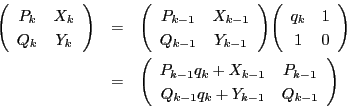
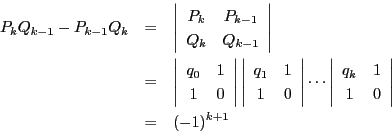
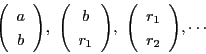
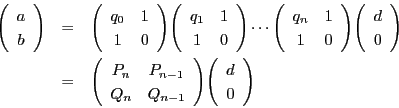
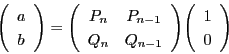
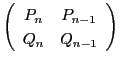 の逆行列を左からかけると,
の逆行列を左からかけると,
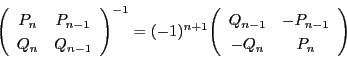
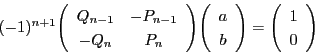
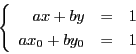

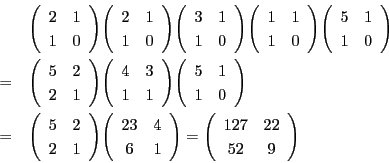
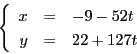
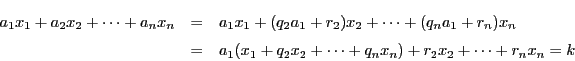
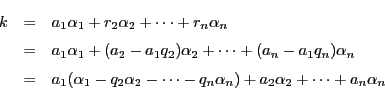
![]() 変数の不定方程式は一般解が構成できる.
係数 0 の未知数を新たな任意整数におく.
こうして得られた一般解から上の手順でもとの方程式の解を構成していけば,
必ずもとの不定方程式の解が構成される.□
変数の不定方程式は一般解が構成できる.
係数 0 の未知数を新たな任意整数におく.
こうして得られた一般解から上の手順でもとの方程式の解を構成していけば,
必ずもとの不定方程式の解が構成される.□