

 次: 素因数分解
上: 素数
前: 素数
次: 素因数分解
上: 素数
前: 素数
本節では素数に関する基礎を学ぶ.
自然数はある意味では単純に定義される.
和,差,積の演算も,約数,倍数の概念も自然なものである.
ところが,1とそれ自身以外には約数をもたない数として定義される素数はかぎりなく奥が深い.素数はいまもってあるいはいよいよ人間にとって神秘な世界である.
実際次のような問題が未解決である.
- [ゴールドバッハの問題]任意の自然数(
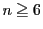 )は,
)は,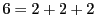 ,
,
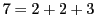 ,
,
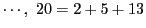 のように常に三つの素数の和に表せるか.
のように常に三つの素数の和に表せるか.
- 任意の偶数は,
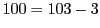 ,
,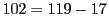 のように常に二つの素数の差で表せるか.
のように常に二つの素数の差で表せるか.
- [双子素数の問題](11と13),(17と19),(29と31)のように
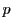 と
と 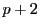 がどちらも素数となるような組は無限にあるか.
がどちらも素数となるような組は無限にあるか.
- [メルセンヌ数]
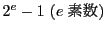 の形をした素数は無数にあるか.
の形をした素数は無数にあるか.
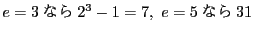 ところが
ところが
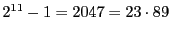
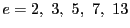 などは素数であるが
などは素数であるが 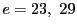 などは素数にならず,
などは素数にならず,
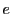 が大きくなるとめったに素数は出てこない.
が大きくなるとめったに素数は出てこない.
- [フェルマ数]
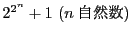 の形をした素数は無数にあるか.
の形をした素数は無数にあるか.
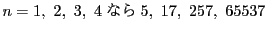 は素数,
は素数,
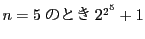 は641で割れる
は641で割れる
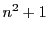 の形をした素数は無数にあるか.また与えられた自然数
の形をした素数は無数にあるか.また与えられた自然数 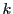 に対して
に対して
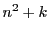 の形をした素数は無数にあるか.
の形をした素数は無数にあるか.
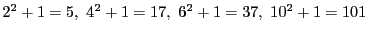 などいくらでもできそうだが,
無限にあるかどうかはわからない.
などいくらでもできそうだが,
無限にあるかどうかはわからない.
このほかに「リーマン予想」と呼ばれる決定的な問題が未解決である.
これらはいずれも当面解けるめどはまったくない.
高校で習う整数というのは,こういう整数の世界の大海のほんの一滴である.
基本事項を練習問題として多数掲載した.
本節では整数の約数,倍数を考えるので,正の数について考えればよい.以下特に断ることなく文字で整数を表すときは,正の整数,つまり自然数であるとする.
定義 4
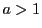
の整数

は少なくとも1と

自身の二つの約数を持つ.
1および

以外の約数を「真の約数」ともいう.
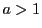
の整数

が真の約数を持たないとき

を
素数 という.
逆に真の約数を持つ整数を
合成数 という.■
整数を,どのような約数を持つかという観点から分類すると,四種類に分かれる.
整数 に対して
に対して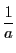 のことを逆数という.
整数のなかで
のことを逆数という.
整数のなかで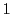 と
と 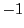 は「逆数もまた整数である」という性質を持つ.
逆数もまた整数である数を単数という.
有理整数の世界では
は「逆数もまた整数である」という性質を持つ.
逆数もまた整数である数を単数という.
有理整数の世界では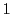 と
と 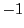 の二つのみが「単数」である.
の二つのみが「単数」である.
Aozora Gakuen

![]() に対して
に対して![]() のことを逆数という.
整数のなかで
のことを逆数という.
整数のなかで![]() と
と ![]() は「逆数もまた整数である」という性質を持つ.
逆数もまた整数である数を単数という.
有理整数の世界では
は「逆数もまた整数である」という性質を持つ.
逆数もまた整数である数を単数という.
有理整数の世界では![]() と
と ![]() の二つのみが「単数」である.
の二つのみが「単数」である.