証明
2以上の整数![]() に関する数学的帰納法で示す.
に関する数学的帰納法で示す.
(1)
![]() のとき
のとき![]() と素数1個の積なので成立.
と素数1個の積なので成立.
(2)
![]() よりも小さい2以上の整数については定理が成立していると仮定する.
よりも小さい2以上の整数については定理が成立していると仮定する.
![]() の分解の可能性を示す.
の分解の可能性を示す.
![]() が素数なら
が素数なら![]() 自身が素数1個の積である.
自身が素数1個の積である.
![]() が合成数のとき.
が合成数のとき.
![]() の分解の一意性を示す.
の分解の一意性を示す.
![]() を素因数に分解して二つの分解
を素因数に分解して二つの分解
(3) (1)(2)より,2以上の任意の整数に対して定理が成立することが示された.□
これは除法を用いていない.自然数の集合には最小のものが存在することだけを用いている.因数分解の可能性は同様なので,一意性のみ別証明をおこなう.
証明
異なる素因数分解をもつ自然数の集合を考える.
この集合に属する最小の自然数を![]() とする.
とする.
![]() は相異なる二つの因数分解をもつ.それを
は相異なる二つの因数分解をもつ.それを
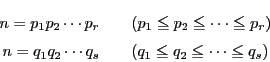
また,
![]() のいずれも
のいずれも
![]() のいずれとも異なる.
なぜなら,もし
のいずれとも異なる.
なぜなら,もし![]() なら,
これを約せば
なら,
これを約せば![]() より小さい数で,異なる因数分解をもつ自然数が得られ,
より小さい数で,異なる因数分解をもつ自然数が得られ,
![]() がそのような数のなかで最小であることに反する.
がそのような数のなかで最小であることに反する.
![]() とする.
ここで自然数
とする.
ここで自然数![]() を
を
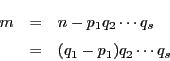
この![]() の因数分解における因数
の因数分解における因数![]() は
は![]() の倍数ではない.
なぜならもし
の倍数ではない.
なぜならもし![]() の倍数なら
の倍数なら![]() が
が![]() の倍数となり互いに異なる素数であることに反する.
よってこの因数分解に
の倍数となり互いに異なる素数であることに反する.
よってこの因数分解に![]() は現れない.
は現れない.
一方![]() は
は
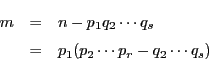
よって![]() の二つの因数分解は相異なる因数分解である.
の二つの因数分解は相異なる因数分解である.
![]() なので,
なので,
![]() が異なる二つの因数分解をもつ最小の自然数であることと矛盾した.
が異なる二つの因数分解をもつ最小の自然数であることと矛盾した.
したがって異なる二つの因数分解をもつ自然数は存在しない.□
除法の原理自身,除法が一意に出来ることを示すためには自然数の集合に最小のものが存在することを用いた.だから,除法を使うか使わないかにかかわらず,自然数の性質が土台になっている.だから,このツェルメロの証明は,自然数の集合には最小のものが存在することをいったん除法の原理にまとめることをせず,自然数の性質から直接示す,ともいえる.
一方,整数![]() 素数であることを,
素数であることを,
どのように論を構成するかという問題よりも,どのような数学的現象とどのような数学的現象が同値であるかを確認することが重要である. このような問題は整域における整除問題として, 環の一般論のなかで諸定義相互の関係は明らかにされる.
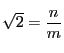 とおく.これから
とおく.これから
素数は無限に存在するのだろうか.この問題の解明は本質的にはユークリッドによってなされた.ユークリッドは『原論』のなかで,素数の個数が3個であるとして矛盾が起こるという形で議論した.つまり背理法である.ユークリッドは歴史に残る人のなかで,はじめて背理法を用いた人である.
証明
背理法で示す.素数の個数が有限であると仮定する.その個数を ![]() 個とし,
個とし,
![]() をすべての素数とする.
このとき
をすべての素数とする.
このとき
定理39 より![]() は素数の積に分解される.
一方
は素数の積に分解される.
一方![]() は
は
![]() のいずれで割っても1余る.
つまり,
のいずれで割っても1余る.
つまり,
![]() は
は![]() の約数でない.
よって
の約数でない.
よって![]() の素因数分解に現れる素数は
の素因数分解に現れる素数は
![]() ではあり得ず,
それら以外の素数である.
これは
ではあり得ず,
それら以外の素数である.
これは
![]() がすべての素数という仮定と矛盾する.
ゆえに素数の数は無限である.□
がすべての素数という仮定と矛盾する.
ゆえに素数の数は無限である.□