

 次: 一次合同方程式
上: 合同式
前: 合同式
次: 一次合同方程式
上: 合同式
前: 合同式
整数 と
と の差が
の差が の倍数であるとき,
の倍数であるとき,
 と
と  は
は  を法として互いに合同であるといい,次のように記す.
を法として互いに合同であるといい,次のように記す.
ここで整数の部分集合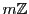 を
を
とする.集合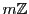 の要素の和・差・積はふたたび
の要素の和・差・積はふたたび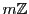 に属する.
合同という関係はこれを用いて
に属する.
合同という関係はこれを用いて
と集合論的にとらえることができる.
定理 9
整数

と

が

を法として合同であることと,

と

を

で割った二つの余りが等しいことは同値である.■
証明
整数 と
と が
が を法として合同であるとし,
を法として合同であるとし,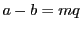 とおく.
ここで
とおく.
ここで と
と を
を で割った商と余りをそれぞれ
で割った商と余りをそれぞれ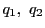 ,
,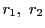 とする.
とする.
辺々引いて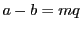 を用いると
を用いると
つまり
もし
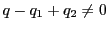 なら,
なら,
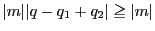 であるが,
右辺は
であるが,
右辺は  で割った余りの差なので
で割った余りの差なので 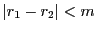 である.
これは矛盾である.
である.
これは矛盾である.
 を法として合同な二数は
を法として合同な二数は で割った二つの数の余りが等しい.
で割った二つの数の余りが等しい.
逆に と
と を
を で割った余りが等しいとする.
で割った余りが等しいとする.
より
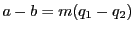 である.つまり
である.つまり と
と は
は を法として合同である.
□
を法として合同である.
□
集合 の要素の間に,成り立つか成り立たないかがつねに確定する関係が定義されているとする.要素
の要素の間に,成り立つか成り立たないかがつねに確定する関係が定義されているとする.要素 と
と の間にこの関係が成り立つことを
の間にこの関係が成り立つことを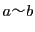 と表す.
と表す.
- (i)
 .
.
- (ii)
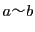 なら
なら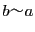 .
.
- (iii)
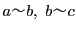 なら
なら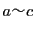 .
.
が成り立つとき,「〜」を「同値関係」という.
例 2.1.1

を整数とする.整数
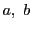
について関係
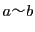
を
で定める.〜は同値関係である.
同値関係があると,同値なものをひとつの部分集合にまとめることができる.
つまり の要素
の要素 と同値な要素からなる
と同値な要素からなる の部分集合
の部分集合
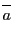 が一意に確定し,
が一意に確定し,
 のすべての要素はいずれかただひとつの
のすべての要素はいずれかただひとつの
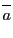 に属する.
いいかえると,任意の
に属する.
いいかえると,任意の
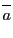 と
と
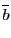 について
について
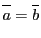 か
か
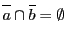 のいずれか一方が成立する.
のいずれか一方が成立する.
 の属する部分集合
の属する部分集合
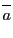 を
を の同値類という.このようにして得られる同値類の集合
の同値類という.このようにして得られる同値類の集合
を,集合 の関係〜に関する商集合という.
の関係〜に関する商集合という.
反射律,対称律は明らかである.推移律も
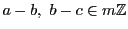 なら
なら
より成立する.
つまり合同という関係は同値関係である.
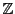 において,
において, を法として互いに合同な整数で一つの部分集合を作り,合同でないものは異なる部分集合になるようにして,
を法として互いに合同な整数で一つの部分集合を作り,合同でないものは異なる部分集合になるようにして,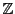 を互いに共通部分のない,いくつかの部分集合の和にすることができる.その一つ一つの部分集合を
を互いに共通部分のない,いくつかの部分集合の和にすることができる.その一つ一つの部分集合を を法とする類といい,類に分けることを類別という.
を法とする類といい,類に分けることを類別という. を法とする類とは,
を法とする類とは, を法として互いに合同なすべての数の集合である.いいかえると
を法として互いに合同なすべての数の集合である.いいかえると で割ったとき余りの等しい整数の集合である.つまり整数を
で割ったとき余りの等しい整数の集合である.つまり整数を で割った余りで類別したのである.それぞれの部分集合を剰余類という.
で割った余りで類別したのである.それぞれの部分集合を剰余類という.
剰余類の集合は,整数の集合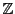 の合同という同値関係による商集合である.これを
の合同という同値関係による商集合である.これを
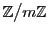 と表す.あるいは
と表す.あるいは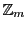 と表すこともある.
と表すこともある. を法とする類別では
を法とする類別では 個の類に類別される.したがって
個の類に類別される.したがって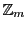 は
は 個の要素からなる集合である.
個の要素からなる集合である.
 を法として
を法として  個に分けられた各集合から一つずつ代表を取り出したとき,それを
完全な代表の一組(または剰余系)という.
例えば
個に分けられた各集合から一つずつ代表を取り出したとき,それを
完全な代表の一組(または剰余系)という.
例えば
はいずれも7を法とする完全な代表の一組になっている.
定理 10
ならば
一般に
で
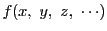
が
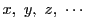
に関する整数係数の整式ならば
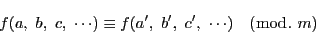 |
(2.2) |
が成り立つ.■
証明
仮定によって
ゆえに
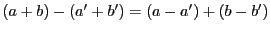 は
は  の倍数である.また,
の倍数である.また,
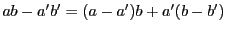 も
も  の倍数である.すなわち(2.1)が示された.
の倍数である.すなわち(2.1)が示された.
(2.1)から
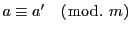 なら任意の整数
なら任意の整数 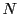 に対して
に対して
および
ふたたび(2.1)から
すなわち (2.2)が示された.□
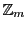 において整数
において整数 の属する類を
の属する類を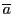 と表す.
と表す. を明示する必要があるときは
を明示する必要があるときは
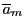 と表そう.本定理の意味することは,
と表そう.本定理の意味することは,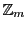 における和と積を
における和と積を
で適切に定義することができる,ということである.つまり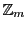 の各類からどのように整数を選んで演算を考えても同じ結果になる.選び方によらず類のみで定まる類と類の間の演算が定義される.そして,分配法則
の各類からどのように整数を選んで演算を考えても同じ結果になる.選び方によらず類のみで定まる類と類の間の演算が定義される.そして,分配法則
も成り立つ.加法と乗法の単位元は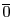 と
と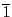 である.これによって
である.これによって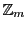 は有限個(
は有限個( 個)の要素からなる環である.
個)の要素からなる環である.
例 2.1.2
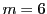
のとき.
演算:
ただし,
なので乗法の逆元が存在するとはかぎらない.
乗法の逆元が存在すれば環は体になる.有理数体,実数体,複素数体はすべて四則演算ができる体であった.これらの体は,無数の要素からなっている.それに対して有限個の要素からなる体が存在する.これはガロアの発見であるが,現代の代数学の扉を開けるものであった.
定理 11

を素数とする.
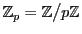
は

個の要素からなる体である.
■
証明
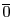 でない他の
でない他の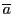 に積の逆元が存在することを示せばよい.
に積の逆元が存在することを示せばよい. として1から
として1から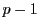 のいずれかをとることができる.このとき
のいずれかをとることができる.このとき と
と は互いに素になる.したがって
は互いに素になる.したがって
となる整数 が存在する.ところが
が存在する.ところが
であるから,
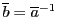 となり
となり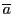 に逆元が存在した.よって
に逆元が存在した.よって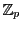 は体である.
□
は体である.
□
このように,剰余類という整数の部分集合を一つの要素と見なし,剰余類にあいだの演算を考える.ここが難しいところであり,また数学が現代に飛躍するところでもあった.今後,本質的なところではこの考え方で考察をすすめるが,必ずしも本質的でないところでは,古典的な考え方でいくようにしたい.


 次: 一次合同方程式
上: 合同式
前: 合同式
Aozora Gakuen
次: 一次合同方程式
上: 合同式
前: 合同式
Aozora Gakuen
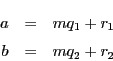
![]() と
と![]() を
を![]() で割った余りが等しいとする.
で割った余りが等しいとする.
![]() の属する部分集合
の属する部分集合
![]() を
を![]() の同値類という.このようにして得られる同値類の集合
の同値類という.このようにして得られる同値類の集合
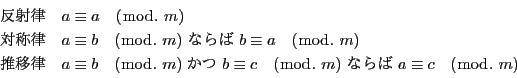
![]() の合同という同値関係による商集合である.これを
の合同という同値関係による商集合である.これを
![]() と表す.あるいは
と表す.あるいは![]() と表すこともある.
と表すこともある.![]() を法とする類別では
を法とする類別では![]() 個の類に類別される.したがって
個の類に類別される.したがって![]() は
は![]() 個の要素からなる集合である.
個の要素からなる集合である.
![]() を法として
を法として ![]() 個に分けられた各集合から一つずつ代表を取り出したとき,それを
完全な代表の一組(または剰余系)という.
例えば
個に分けられた各集合から一つずつ代表を取り出したとき,それを
完全な代表の一組(または剰余系)という.
例えば
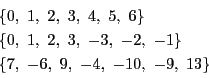

![]() なら任意の整数
なら任意の整数 ![]() に対して
に対して
![]() において整数
において整数![]() の属する類を
の属する類を![]() と表す.
と表す.![]() を明示する必要があるときは
を明示する必要があるときは
![]() と表そう.本定理の意味することは,
と表そう.本定理の意味することは,![]() における和と積を
における和と積を
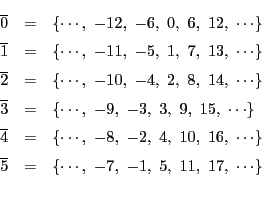
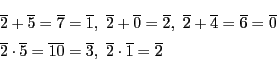
![]() でない他の
でない他の![]() に積の逆元が存在することを示せばよい.
に積の逆元が存在することを示せばよい.![]() として1から
として1から![]() のいずれかをとることができる.このとき
のいずれかをとることができる.このとき![]() と
と![]() は互いに素になる.したがって
は互いに素になる.したがって